Start | trad
 

Träd



Ett träd är en datastruktur som efterliknar hur träd ser ut. Vi har en stam (root) som förgrenar sig i grenar som förgrenar sig i ännu mer grenar och ytterst sitter ett löv.

egenskaper

Om man tänker sig att en länkad lista's kännetecken är att om du befinner dig i en nod, så finns där en node.next, som leder till nästa nod, såtillvida inte node.next är None. Och du kan enkelt i en länkad lista, genom att koppla om node.next, montera in en ny nod mellan två existerande. Eller ta bort en nod genom att koppla förbi den.

Ett träd fungerar likadant, fast du har här två eller fler noder med vars hjälp du kan vandra ut i trädet. Om det är två noder (binärt träd) heter de oftast left och right. Så node.left leder till vänster delträd och node.right leder till högra. Om det är ett träd med godtyckligt många grenar (förgreningar), så ligger oftast alla grenar i en lista med namnet children och du kan komma åt grenarna genom att loopa över children.

Denna enkla introduktion till träd handlar om träd med godtyckligt många grenar.



Notera symmetrierna i ett träd. Vi kan klippa ut ett delträd (subtree) och det nya delträdet vi klippt ut har då fått en ny root. Rooten är bra hålla reda på, det är dels själva pekaren till trädet men också där trädet börjar.

Notera också hur en parent (förälder) har children (barn).

Varje nod kan t.ex. innehålla en lista med alla children. Dvs, om vi befinner oss i en nod, då kan vi loop:a över alla children. Notera att en typisk child kan vara parent till nya children.

Löven längst ut på trädet kännetecknas av att de saknar children. Listan med children är None.

Så, vill vi vandra nedåt i trädet kan vi göra det genom alla children. En typisk nod har ofta pekare till sin parent, så att vi även skall kunna vandra uppåt i trädet. Rooten har ingen parent, så vi känner igen rooten genom att parent är None.

En nod innehåller oftast någon typ av data. Hur många barn (förgreningar) en nod har kallas också för nodens grad. Så, en nod med 2 barn är av grad 2. Trädets grad räknas ut genom att titta på den nod som har högst grad (dvs flest barn, förgreningar, children = kärt barn har många namn!).

Det var en snabb genomgång av de flesta begrepp. Repetera nu för dig själv; Träd, rot, subträd, nod, förälder, barn, children, parent, löv, förgreningar, noden och trädets grad. Om du begriper dessa någorlunda har du kommit långt!

Typer av träd


Det finns många olika sorters träd och vad man väljer beror förstås på vad man behöver. Exempel på träd är binära träd, AVL (självbalanserande binära träd), heap, osv.

enkelt träd


Låt oss skapa ett enkelt träd. Vi tar fasta på att varje nod innehåller data samt en lista med children, ifall sådana existerar. Dessa children är i sin tur en nod som kan ha children o.s.v. i all evighet.
class Node: def __init__(self, data=None, children=None): self.data = data self.children = children if children is not None else [] def print_tree(tree, d=0): if(tree): print("\n" + " "*d + '('+str(tree.data)+')',end="->") if tree.children: for child in tree.children: print_tree(child,d+1) game = Node('1') print_tree(game)
I begynnelsen är trädet väldigt litet. Men vi kan enkelt bygga ut trädet. Vi kan skapa trädet direkt med vår klass Node eftersom våra barn ligger i en lista.

undvika delad lista


Det är lätt att tänka tanken konstruera en Node såhär
class Node: def __init__(self, name="", data=None, children=[]): self.name = name self.data = data self.children = children
Om du inte genast börjar tvivla på denna konstruktion, ta en kort paus och gå igenom en kort sida om problemet med default argument och listor. När du gjort det, så är konstruktionen nedan glasklar.
class Node: def __init__(self, name="", data=None, children=None): self.name = name self.data = data self.children = children if children is not None else [] def print_tree(tree, d=0): if(tree): print("\n" + " "*d + tree.name + '('+str(tree.data)+')',end="->") if tree.children: for child in tree.children: print_tree(child,d+1) game1 = Node('a','1', [Node('b','2'), Node('c','3')]) game2 = Node('d','4', [game1, Node('e','5'), Node('f','6')]) print_tree(game2)
För att hjälpa dig koda och labba med träd, här har du ytterligare en utskriftsfunktion av trädet som du kan kopiera. Du behöver kunna printa ut trädet för att labba och lära, men att göra en snygg utskriftsfunktion kräver en hel del insikter, så det är ett moment 22.
class Node: def __init__(self, name="", data=None, children=[]): self.name = name self.data = data self.children = children def print_tree(root, prefix="", is_last=True): print(prefix, "└─ " if is_last else "├─ ", root.name, ": ", root.data, sep="") prefix += " " if is_last else "│ " child_count = len(root.children) for i, child in enumerate(root.children): is_last_child = (i == (child_count - 1)) print_tree(child, prefix, is_last_child) game1 = Node('a','1', [Node('b','2'), Node('c','3')]) game2 = Node('d','4', [game1, Node('e','5'), Node('f','6')]) print_tree(game2)
Nedan har du ytterligare en avancerad utskriftsfunktion. Den tog några timmar att koda ihop, så använd den nu för bövelen! Du kan säkert ta det ytterligare några nivåer.
class Node: def __init__(self, name="", data=None, children=[]): self.name = name self.data = data self.children = children class Tree: def addNodes(self,r): self.root = r def printNodes(self,node, d=0, lr=''): def cap(x,c): if(x>c): x=c return x if(node==None or node.children is None): return A = node.children B = A[:1+len(A)//2] C = A[1+len(A)//2:] if(B): for i in range(len(B)): self.printNodes(B[i],d+1,'┌' if i==0 else '│') self.c[d] += (1 if lr =='┌' or lr =='│' else -1) if self.c[d]<0: self.c[d]=0 if(lr=='└'): self.c[d]=0 if(lr=='┌'): self.c[d+1]=0 vbrack = ''.join([' ',' │'][cap(self.c[i],1)] for i in range(1,len(self.c)) if i < d) print(vbrack+ ('' if d==0 else ' ') + lr +'──' +'(' +str(node.name)+str(node.data)+')') if(C): for i in range(len(C)): self.printNodes(C[i],d+1,"└" if i == (len(C)-1) else '│') def print(self): self.c = [0 for x in range(20)] self.printNodes(self.root) tree = Tree() game1 = Node('a','1', [Node('b','2'), Node('c','3'), Node('c','3'), Node('c','3'), Node('c','3')]) game2 = Node('d','4', [game1, Node('e','5',[game1,game1,game1]), Node('f','6',[game1])]) tree.addNodes(game2) tree.print()

Traversering av träd

Beroende på vad vi vill göra, så vill vi traversera trädets noder i olika ordning.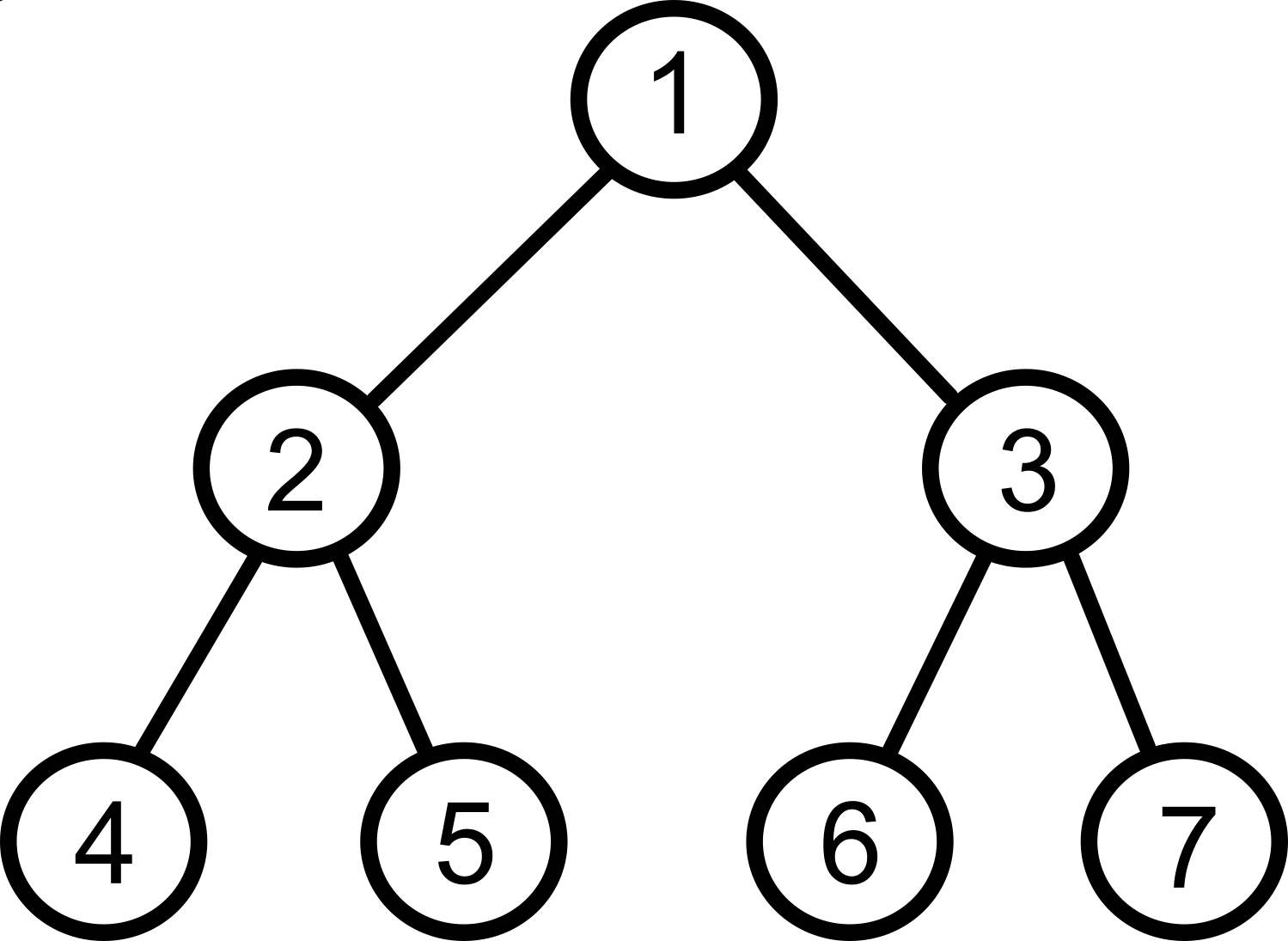

in-order
4251637
pre-order
1245367
post-order
4526731
level-order
1234567

in-order


In-order är vanligtvis bara vettigt om vi har ett binärt träd. Algoritmen är:

1. Gå igenom vänster delträd
2. Beakta rooten (skriv ut eller gör vad du vill)
3. Gå igenom höger delträd

4251637

pre-order


Algoritmen är:

1. Beakta rooten (skriv ut eller gör vad du vill)
2. Gå igenom vänster delträd
3. Gå igenom höger delträd

1245367

post-order


Algoritmen är:

1. Gå igenom vänster delträd
2. Gå igenom höger delträd
3. Beakta rooten (skriv ut eller gör vad du vill)

4526731

level-order


Innebär att vi traverserar noderna nivå för nivå med start från level 0 (rooten). Algoritmen är lite mer komplicerad och förutsätter att vi använder en kö. Vi kan enkelt skapa en kö i python med en lista och använda append (push) samt pop(0) (obs viktigt med 0:an, annars får vi en stack)

1. Skapa en tom kö
2. Placera rooten i kön
3. Loopa sålänge kön innehåller något och gör nedan:
3a. Plocka nod ur kön och beakta denna (skriv ut t.ex.)
3b. Placera nodens barn i kön.

1234567

class Node: def __init__(self, data=None, children=None): self.data = data self.children = children if children is not None else [] # När vi printar trädet är det pre-order def print_tree(tree, d=0): if(tree): print("\n" + " "*d + '('+str(tree.data)+')',end="->") if tree.children: for child in tree.children: print_tree(child,d+1) t = Node('1', [ Node('2', [ Node('4'), Node('5')]), Node('3', [ Node('6'), Node('7')]) ]) print_tree(t) def print_inorder(node): if(node.children): print_inorder(node.children[0]) print(node.data, end="->") print_inorder(node.children[1]) else: print(node.data, end="->") def print_preorder(node): print(node.data, end="->") if(node.children): for child in node.children: print_preorder(child) def print_postorder(node): if(node.children): for child in node.children: print_postorder(child) print(node.data, end="->") def print_levelorder(root): if (not root): return queue = [] queue.append(root) while (len(queue) > 0): node = queue.pop(0) print(node.data, end="->") if(node.children): for child in node.children: queue.append(child) print("\ninorder:") print_inorder(t) print("\npreorder:") print_preorder(t) print("\npostorder:") print_postorder(t) print("\nlevelorder:") print_levelorder(t)

AST exempel

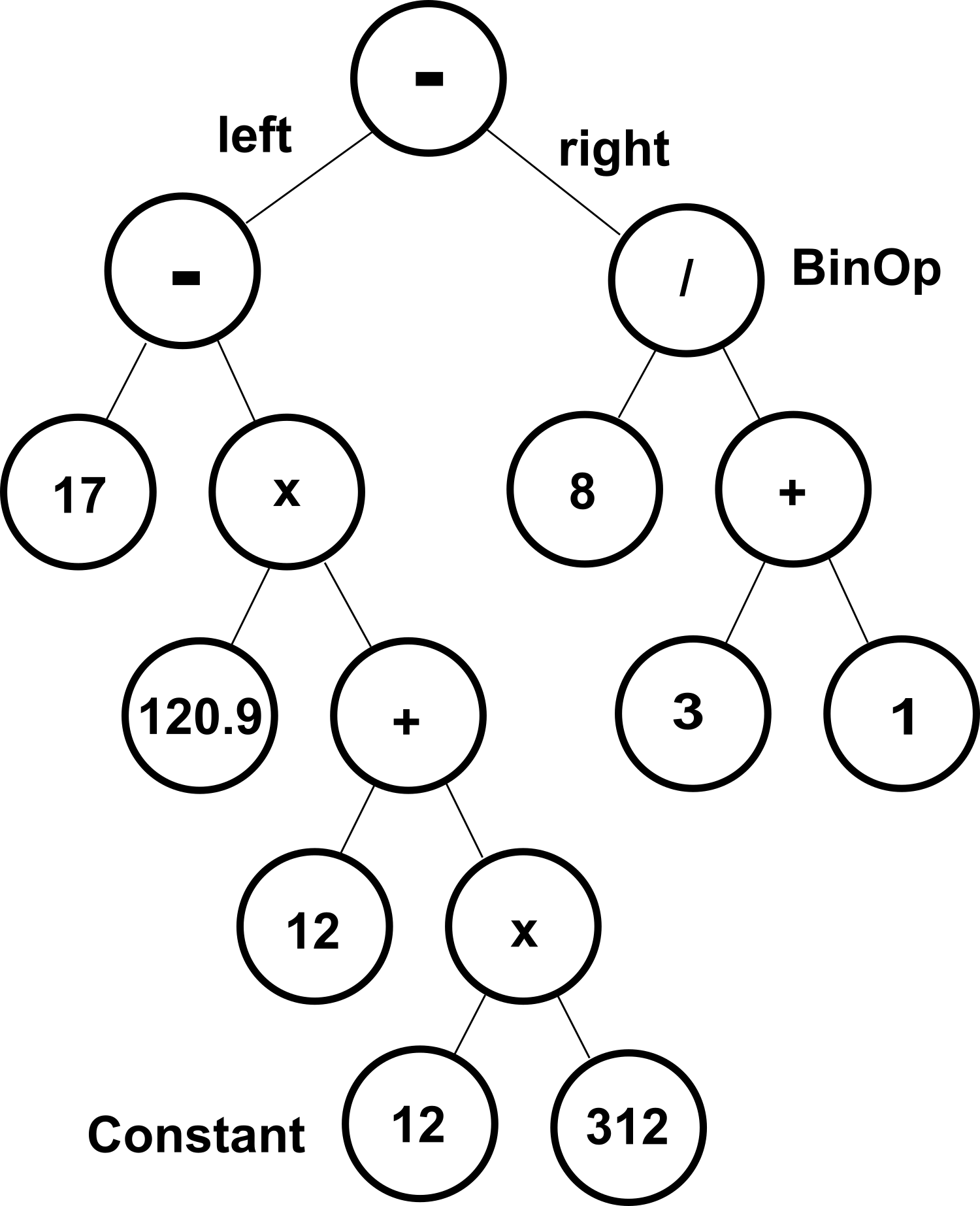
Nedan är ett abstrakt syntaxträd (AST) av uttrycket. Det är python själv som gjort det abstrakta syntaxträdet från ett infix uttryck.

17 - 120.9 * ( 12 + 12 * 312 ) - 8 / ( 3 + 1 )

Vi tar detta träd och matar in det och sedan traverserar vi trädet med de olika metoderna.
class Node: def __init__(self, data=None, children=None): self.data = data self.children = children if children is not None else [] # När vi printar trädet är det pre-order def print_tree(tree, d=0): if(tree): print("\n" + " "*d + '('+str(tree.data)+')',end="->") if tree.children: for child in tree.children: print_tree(child,d+1) t = Node('-', [ Node('-', [ Node('17'), Node('*',[ Node('120.9'), Node('+',[ Node('12'), Node('*',[ Node('12'), Node('312') ]) ]) ])]), Node('/', [ Node('8'), Node('+',[ Node('3'), Node('1') ])]) ]) print_tree(t) def print_inorder(node): if(node.children): print_inorder(node.children[0]) print(node.data, end=" ") print_inorder(node.children[1]) else: print(node.data, end=" ") def print_preorder(node): print(node.data, end=" ") if(node.children): for child in node.children: print_preorder(child) def print_postorder(node): if(node.children): for child in node.children: print_postorder(child) print(node.data, end=" ") def print_levelorder(root): if (not root): return queue = [] queue.append(root) while (len(queue) > 0): node = queue.pop(0) print(node.data, end=" ") if(node.children): for child in node.children: queue.append(child) print("\ninorder:") print_inorder(t) print("\npreorder:") print_preorder(t) print("\npostorder:") print_postorder(t) print("\nlevelorder:") print_levelorder(t)
Skriver vi ut detta på preorder så är det samma sak som prefix notation.

- - 17 * 120.9 + 12 * 12 312 / 8 + 3 1

Postorder är samma sak som postfix notation. 

17 120.9 12 12 312 * + * - 8 3 1 + / -

Inorder är samma sak som den infixa notation vi hade från början, fast i utskriften har parenteser försvunnit. 

17 - 120.9 * ( 12 + 12 * 312 ) - 8 / ( 3 + 1 )

Evaluera AST -trädet kan vi göra med en enkel postorder snurra över trädet.

parent

Ofta i en nod i ett träd, så finns en referens parent som refererar till föräldern. Detta kan göra manipulation eller beräkningar lättare. Vi kan t.ex. enkelt härleda fullständiga vägen från roten till en nod (se findPath nedan).
class Node: def __init__(self, data=None, children=None): self.parent = None self.data = data self.children = children if children is not None else [] for child in self.children: child.parent = self def print_tree(tree, d=0): if(tree): print("\n" + " "*d + '('+str(tree.data)+')',end="->") for child in tree.children: print_tree(child,d+1) def findPath(node, data): path = "" if node.data == data: while(node is not None): path = node.data + '/' + path node=node.parent return path for child in node.children: result = findPath(child, data) if result: return result game = Node('1', [Node('2'), Node('3',[Node('4')])]) print_tree(game) print() print() print("path=",findPath(game, '4'))

insert och delete

Såklart vill vi ofta sätta in eller ta bort noder i trädet. Om vi ska sätta in en ny nod letar vi först reda på noden med find. Därefter hänger vi på ny data där. Delete tar bort en nod. Om noden har barn (children) så omlokaliserar vi dem först så att de inte blir föräldrarlösa.
class Node: def __init__(self, data=None, children=None): self.parent = None self.data = data self.children = children if children is not None else [] for child in self.children: child.parent = self def print_tree(tree, d=0): if tree: print("\n" + " " * d + '(' + str(tree.data) + ')', end="->") if tree.children: for child in tree.children: print_tree(child, d + 1) def insert(parent, data): new_node = Node(data) new_node.children = None new_node.parent = parent parent.children.append(new_node) return new_node def find(node, data): if node.data == data: return node for child in node.children: result = find(child, data) if result: return result return None def delete(node): if node.parent: node.parent.children.remove(node) for child in node.children: child.parent = node.parent node.parent.children.append(child) node.parent = None node.children = [] t = Node('Fritidsaktiviteter', [ Node('Musik', [ Node('Piano'), Node('Mandolin')]), Node('Sport', [ Node('Gräs'), Node('Is',[ Node('Ishockey'), Node('Konståkning') ])]) ]) print_tree(t) node = find(t, 'Ishockey') print("\n\nhittade:",node.data) print("Tar bort denna nod") delete(node) print_tree(t) print("\n\nStoppar in ny nod") node = find(t, 'Is') insert(node, 'Bandy') print_tree(t)
12.564897537231 ms