minmax

Du vill maximera din poäng (minimera motspelarens chanser), men motspelaren vill minimera dina poäng (maximera sina egna chanser). Så, krasst: Hur bra poäng kan du få givet att du kan vara säker på att motspelaren systematiskt saboterar maximalt?

svåra beslut

Tänk dig ett spel, där spel-situationen ges ett antal poäng. Exakt hur poängsättningen går till, med en evalueringsfunktion, är inte viktigt just nu (vi tar det senare) men du kan utgå ifrån att poängen är ganska rättvis. En hög poäng är bra för dig, en låg poäng är dåligt. Det är allt du behöver veta för nu.

Vilket alternativ väljer du? Okej, det är en no-brainer. Du väljer det högsta såklart. 31 poäng!

Säg att du spelar ett spel mot någon. Det kan egentligen generaliseras till lite allt möjligt, men vi håller oss till spel och lek. Det är du och någon annan. I detta spel vill du välja det alternativ som ger dig mest poäng. Problemet är; det vill din motspelare också. Båda vill ha maximalt med poäng.

I själva verket har ni motsatt agenda. Du vill vinna, men det vill din motspelare också. Tittar vi på poängen, så blir det så att mest poäng för dig blir minst poäng för din motspelare och tvärtom.

Du vill maximera dina poäng, dvs minimera motståndarens poäng, men utmanarens ambition att göra detsamma för sig själv, det innebär att motspelaren kommer minimera dina poäng, för att maximer sina egna.

Din fråga till dig själv blir: Vad är det mesta jag kan få, givet att motspelaren försöker sabba (minimera) så mycket det går?

Säg att du har 2 val, det förefaller som om det ena ger mer än det andra. Men du har inte en aning om vad motspelaren tänker göra. Du har inte funderat så mycket på det. Det är därför du har förlorat spelet så många gånger. Så nu har du bestämt dig för att koppla på intelligensblicken och tänka lite. Du gör en tabell över vad motspelaren kan göra för motdrag samt hur mycket poäng det blir. Du kommer fram till följande.
Dvs, du upptäcker att motspelaren kan sabotera för dig. Om du gör draget som du trodde skulle ge dig 31 poäng, så kan motspelaren göra ett motdrag som sänker detta till 1 poäng. Inte så bra. Om du gör draget som såg ut att ge dig 11 poäng, då kan motspelaren sabotera för dig där också. Men du har fortfarande 6 poäng, vilket är bättre än 1 poäng. Du upptäcker att det ser ut såhär:
Dvs, du gör en tabell över det minsta (min) garanterade du kan få för de olika alternativen och sedan väljer du det högsta (max) av dessa. Du finner då att alternativ b är det bästa. Det garanterar dig 6 poäng. Nyckelordet här, det är garantera.

minmax

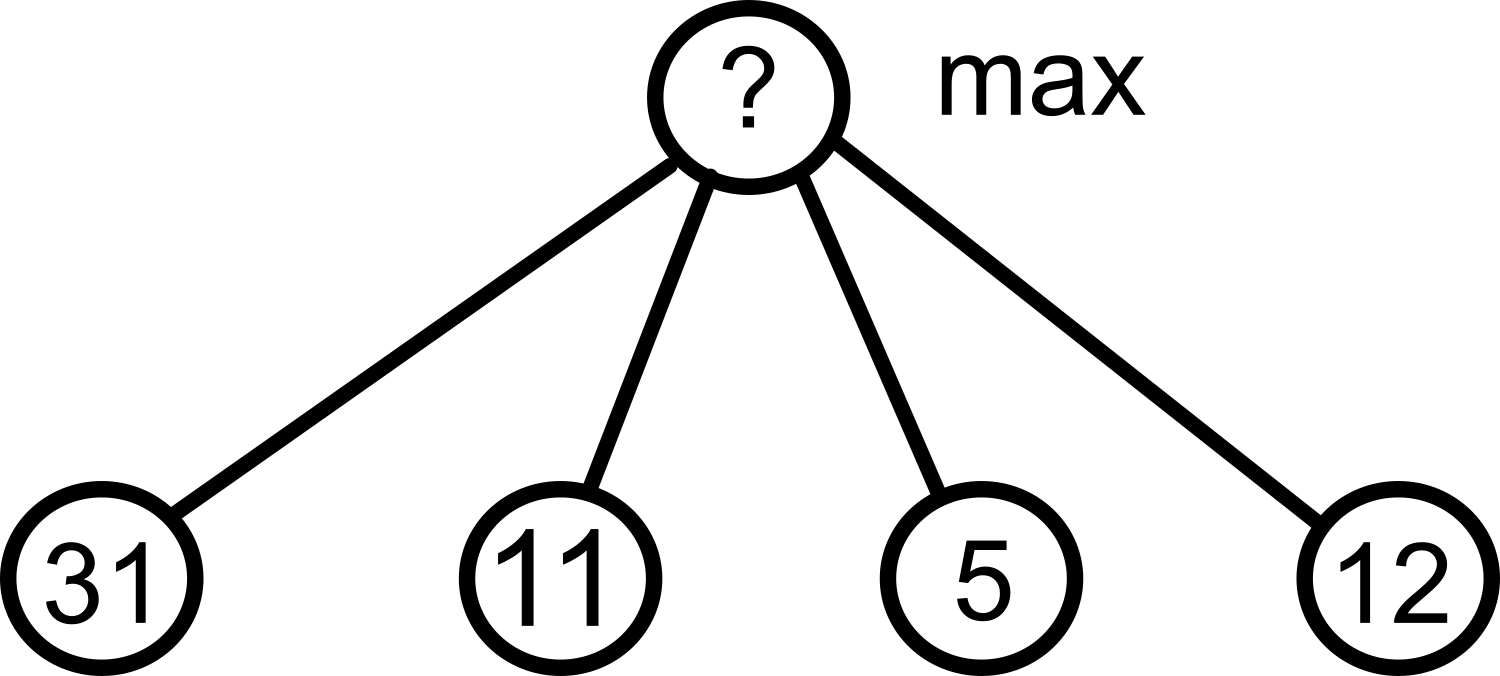
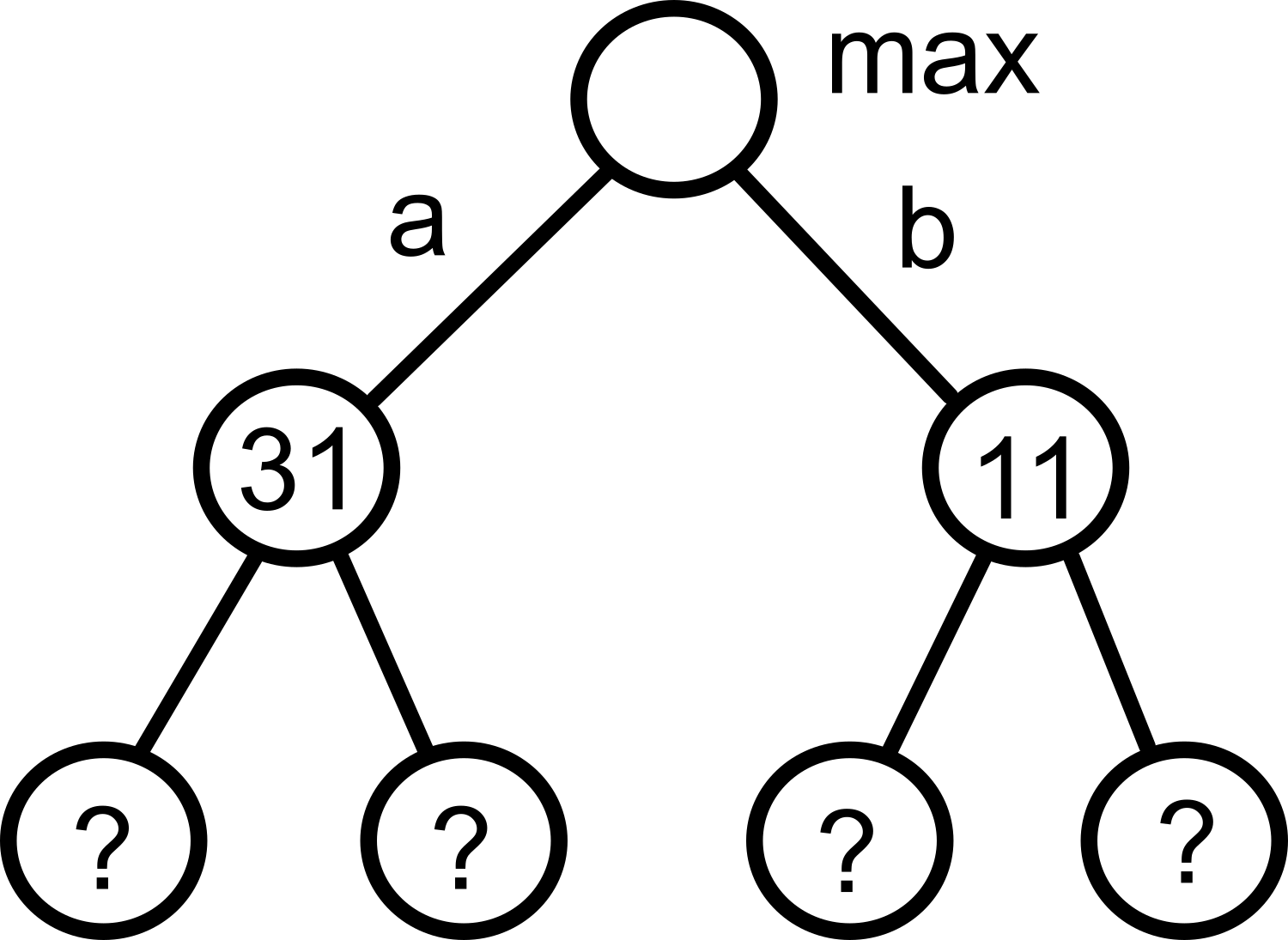
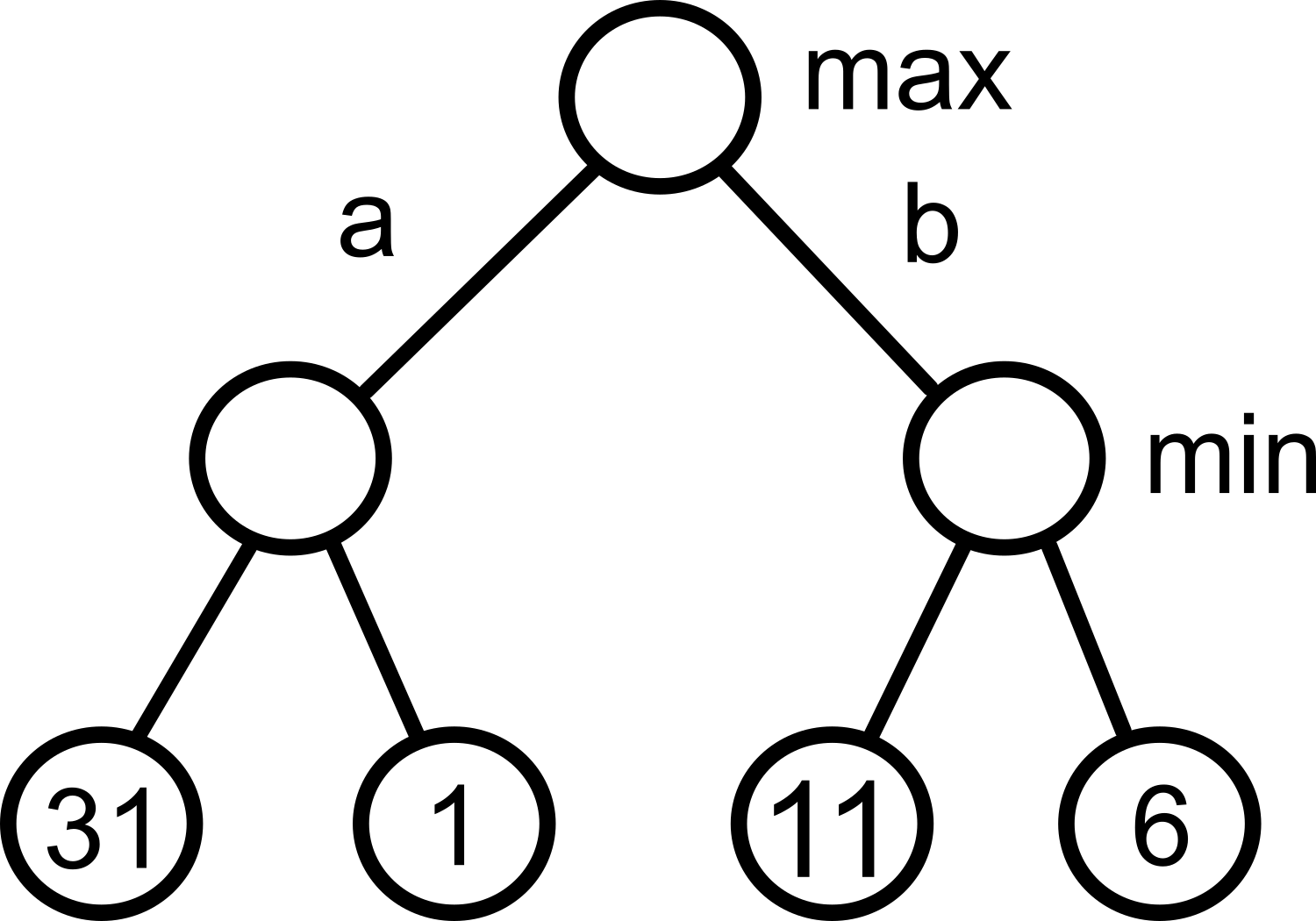
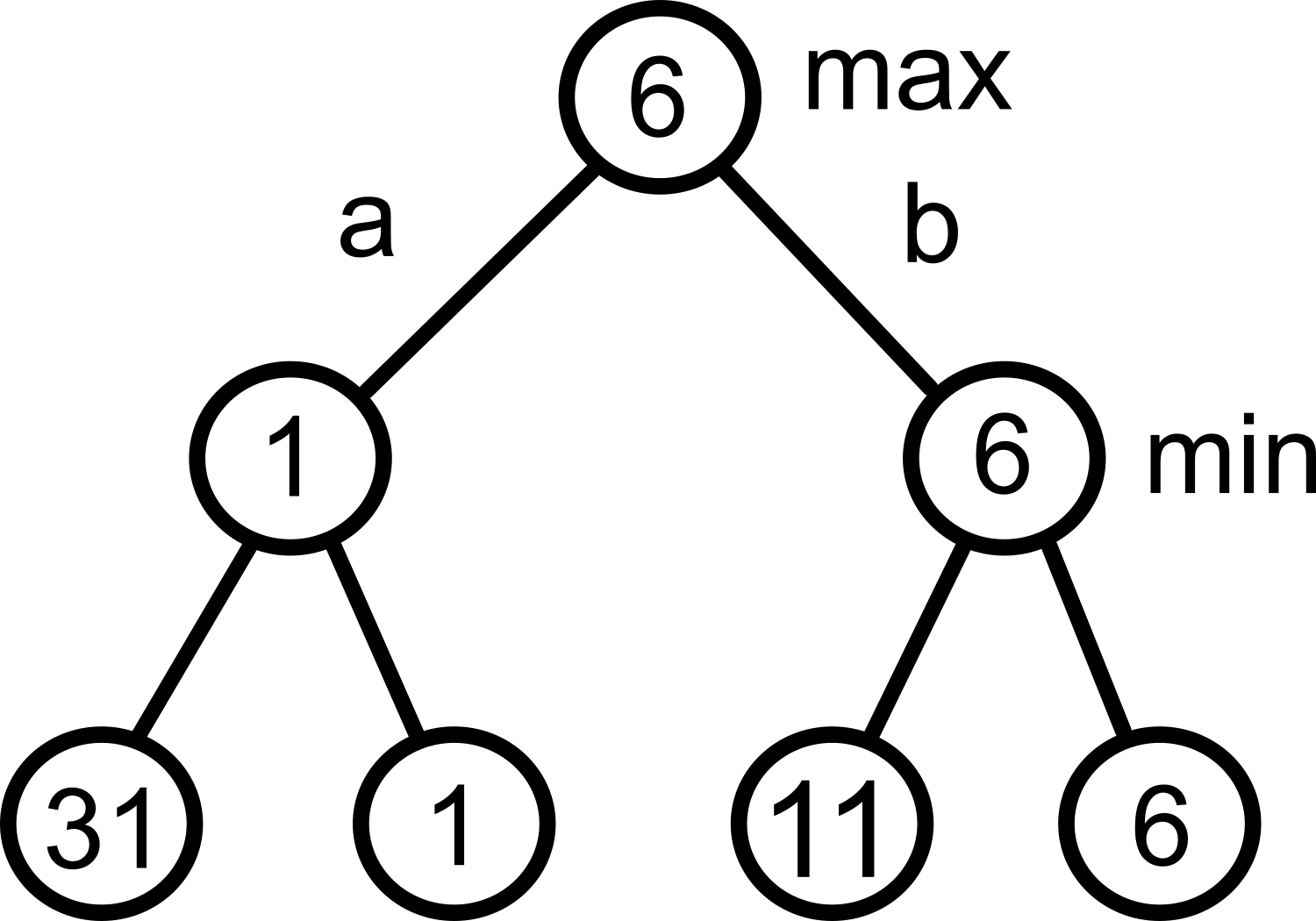
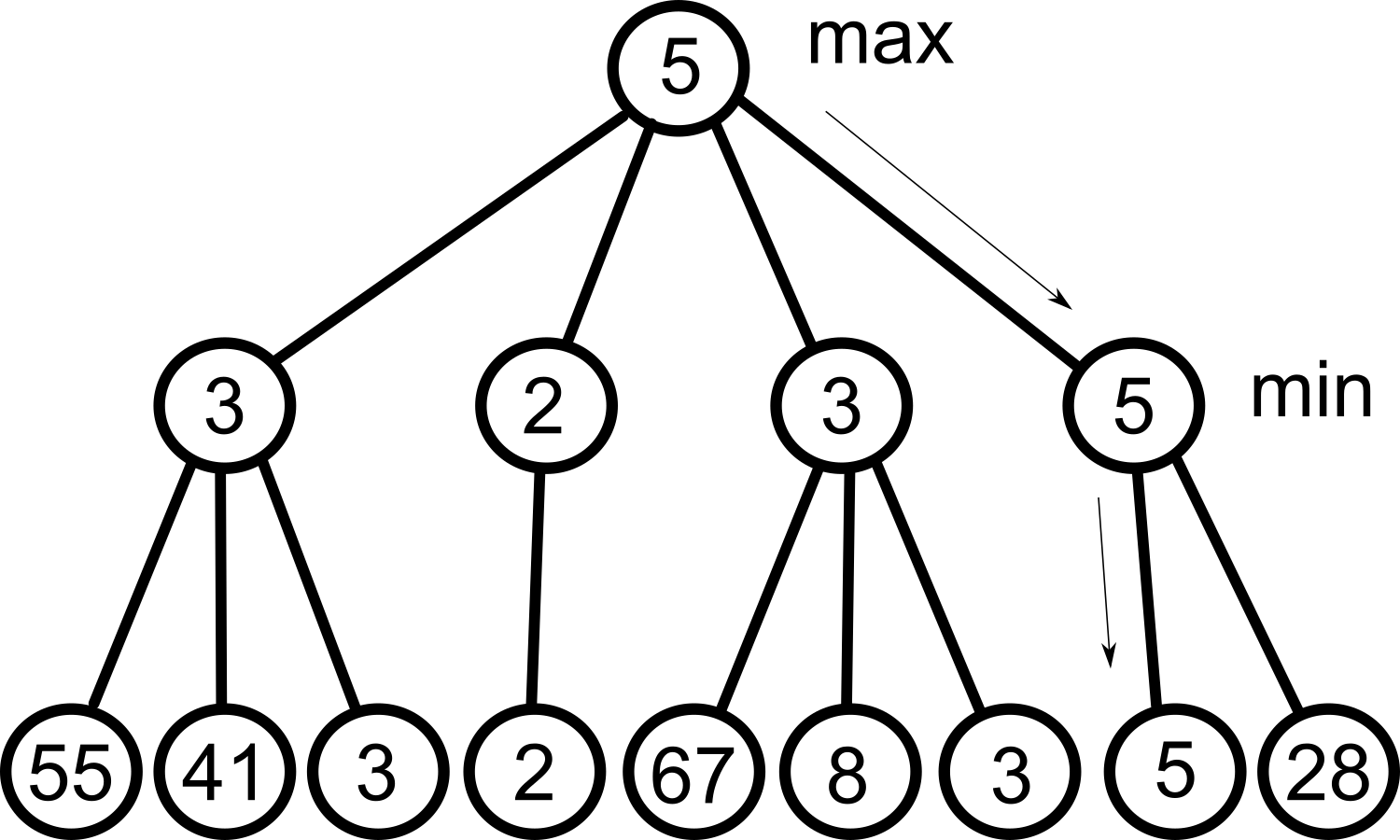
Så, minmax är att vi väljer det drag som ger mest poäng, givet förutsättningen att motspelaren tänker likadant, dvs försöker minimera dina poäng. Genom att välja max och min ömsom varannan nivå, så kan vi vaska fram de poäng som vi är garanterade även om motspelaren gör sitt bästa för att minimera våra poäng.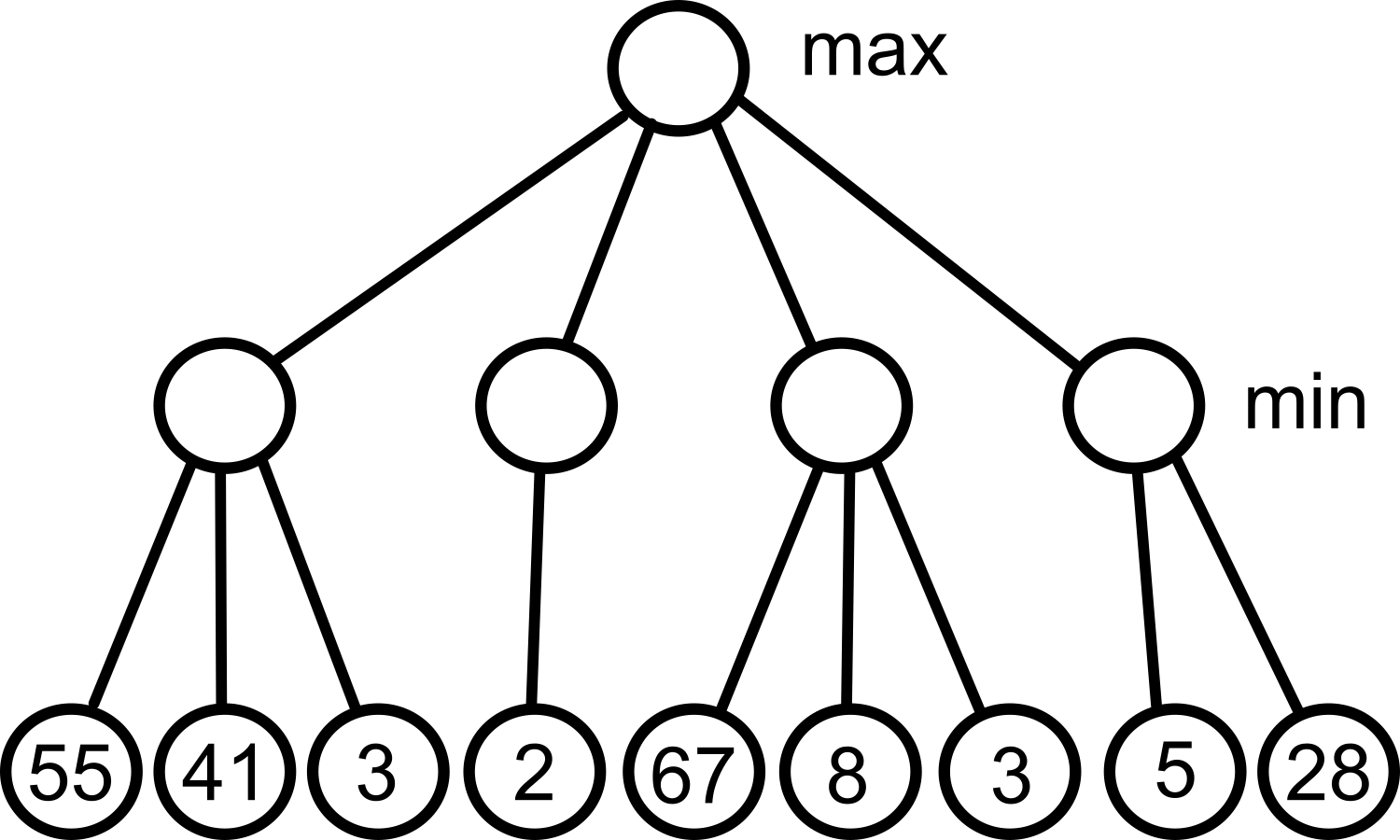 Om vi räknar ut vad motparten kan göra och antar att denne kommer mimimera våra möjligheter, så kan vi fortfarande räkna ut vilket alternativ som garanterar oss högst värde.

pseudokod algoritm

Vi kan snickra ihop en enkel funktion för max med algoritmen vi följer.

1. Vi skapar en lista av alla möjliga drag vi kan göra.
2. Vi gör ett drag i listan, ser vad det blir för poäng.
3. Om det blir mer poäng än tidigare drag, då lägger vi draget på minnet.
4. Vi tar tillbaka draget och om det finns fler drag i listan gå till (2)

Kort sagt, vi provar alla drag, minns poängen och draget som ger högst poäng. Så vi kan skriva pseudokoden som nedan.

def Max(djup, s)
   poang = -99999999
   if (djup <= 0):
      return Eval()
   drag=dragGenerator(s)
   while (drag kvar):
      Gör ett drag i listan
      val = Min(djup-1,1-s)
      Ta tillbaka detta drag
      if (val > poang):
         poang = val
   return poang

På motsvarande sätt kan vi skriva kod för hur motspelaren resonerar.

1. Vi skapar en lista av alla möjliga drag motspelaren kan göra.
2. Vi gör ett drag i listan, ser vad det blir för poäng.
3. Om det blir mindre poäng än tidigare drag, då lägger vi draget på minnet.
4. Vi tar tillbaka draget. Finns det fler drag i listan gå till (2)

Kort sagt, vi provar alla drag, minns poängen och draget som ger lägst poäng. Så vi kan skriva pseudokoden såhär:

def Min(djup, s)
   poang = 99999999
   if (djup <= 0):
      return Eval()
   drag=dragGenerator(s)
   while (drag kvar):
      Gör ett drag i listan
      val = Max(djup-1,1-s)
      Ta tillbaka detta drag
      if (val < poang):
         poang = val
   return poang

Lite kommentarer till kodsnuttarna ovan. Om vi kallar vit respektive svart spelare för 1 och 0, så kan vi pendla mellan spelarna med konstruktionen 1-s. Dvs, om spelaren är 1, så blir blir ju 1-s = 0. Är spelaren 0 så blir 1-s = 1.

För att få fram poängerna i noderna anropar vi ömsom max() och ömsom min(), då varannan nivå (motspelarens tur göra drag) skall hanteras omvänt. Så funktionerna anropar varandra rekursivt. Hur djupt ner i trädet vi går beror helt enkelt på hur många drag i framtiden vill vill söka. När vi nått max djup, då hämtar vi poäng från evalueringsfunktionen. I specialsituationen när vi bara tittar på djup = 1, då kommer anropen till Min() resp Max() att bli ett anrop till Eval() som ger poängen - eller hur?

Vi kan vara finurliga och skriva samman Max och Min i en och samma snurra. Vi kallar den Negamax. Det är ovan 2 algoritmer i en och samma kod.

def NegaMax(djup, s)
   if (djup== 0):
      return Eval()
   drag=dragGenerator(s)
   best = -99999999
   while (drag kvar):
      Gör ett drag i listan
      temp=-Negamax(djup-1,1-s)   
      Ta tillbaka draget
      if (temp>best):
         best=temp
   return best

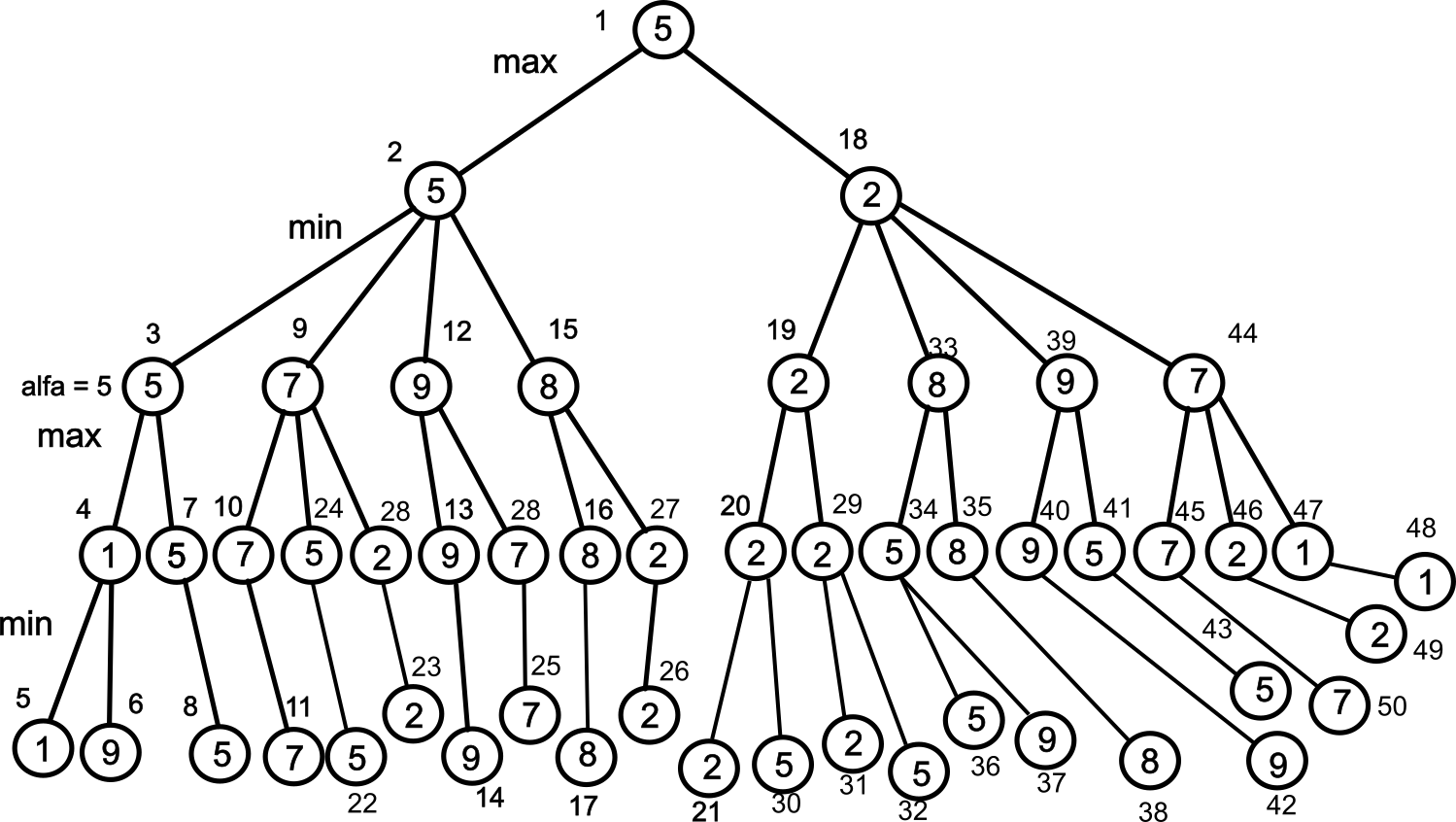
Låt oss skapa ett så stort träd vi orkar knappa in och testa den här negamax! Negamax ska normalt sitta i ett strategispel såklart, men vi kan "simulera" ett strategispel genom att skapa ett träd där löven längst ut har värden, sådana som evalueringsfunktionen i ett riktigt spel hade gett ifrån sig. På så viss kan vi labba lite med ett träd, ändra poäng och se vad som händer.

Observera att i trädet här har jag skrivit ut alla värden ("facit") i noderna. Men koden känner inte till detta. Tittar du på Tree så ser du att enbart löven har poäng. Vi ser att koden räknar ut alla värden korrekt. Ändra i trädet, dvs ändra något poängvärde i löven, och studera resultatet.

Minimax sökningen kan optimeras med alfabeta -reducering.