alfabeta -reducering
Alfabeta -reducering är en optimering av minmax sökalgoritm. Säg att vi hittat ett drag som garanterar oss en viss poäng i ett tidigare delträd. Om vi senare i sökningen kommer till en situation i ett annat delträd där vi kan vara säkra på att vi kommer få samma eller mindre poäng - då kan vi avbryta sökningen i det delträdet (och spara tid). Det är denna grej detta handlar om. Skippa onödig sökning.
skippar onödig sökning
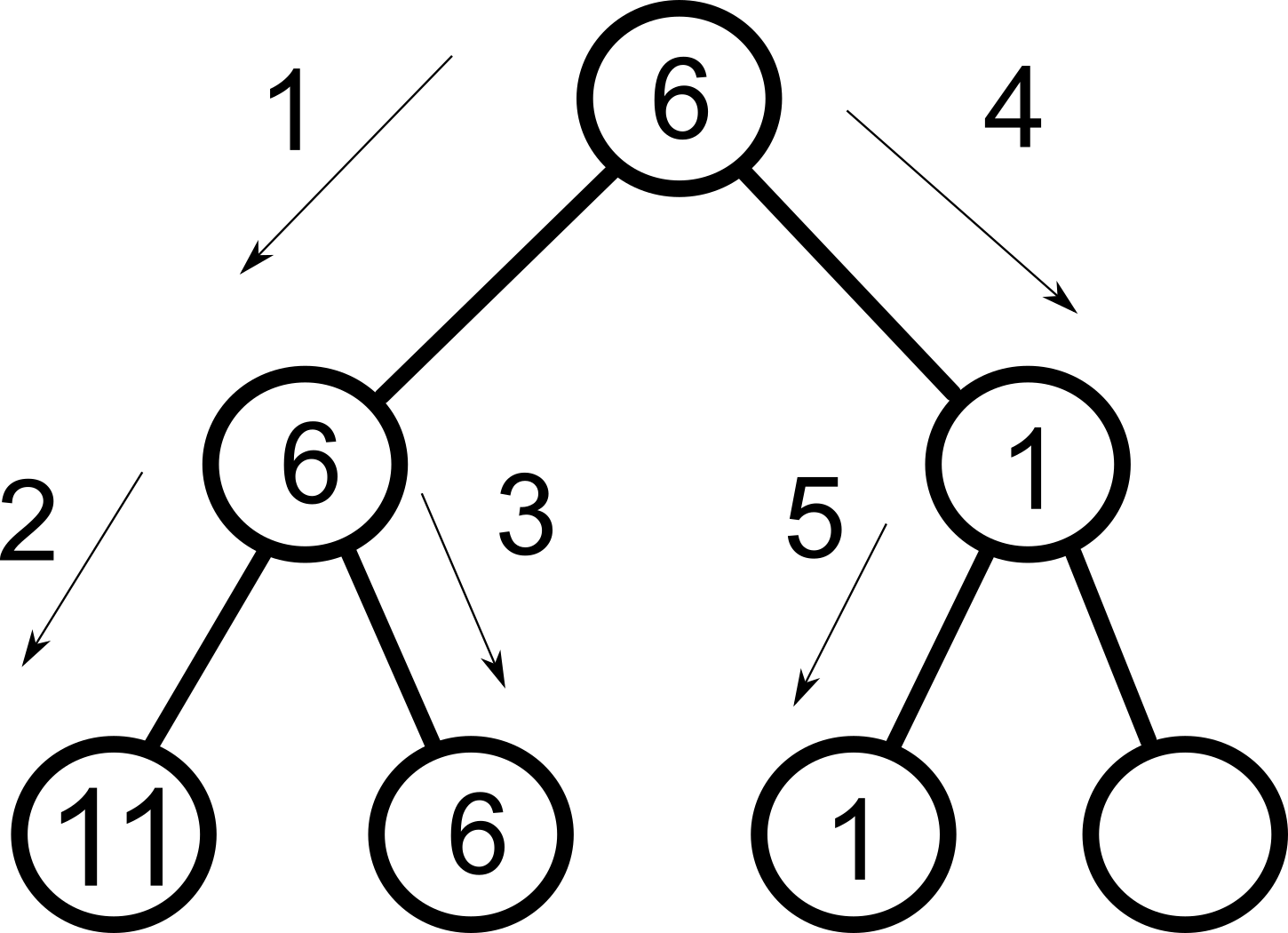
Om det finns ett bra drag och du har hamnat i delträd som i bästa fall ger ett sämre drag - sluta sök i den grenen och gå istället vidare.För att förstå alfabeta -reducering är det hög tid begripa att minmax är av typen djupet-först. Sökalgoritmen söker alltså igenom trädet i nedan ordning.
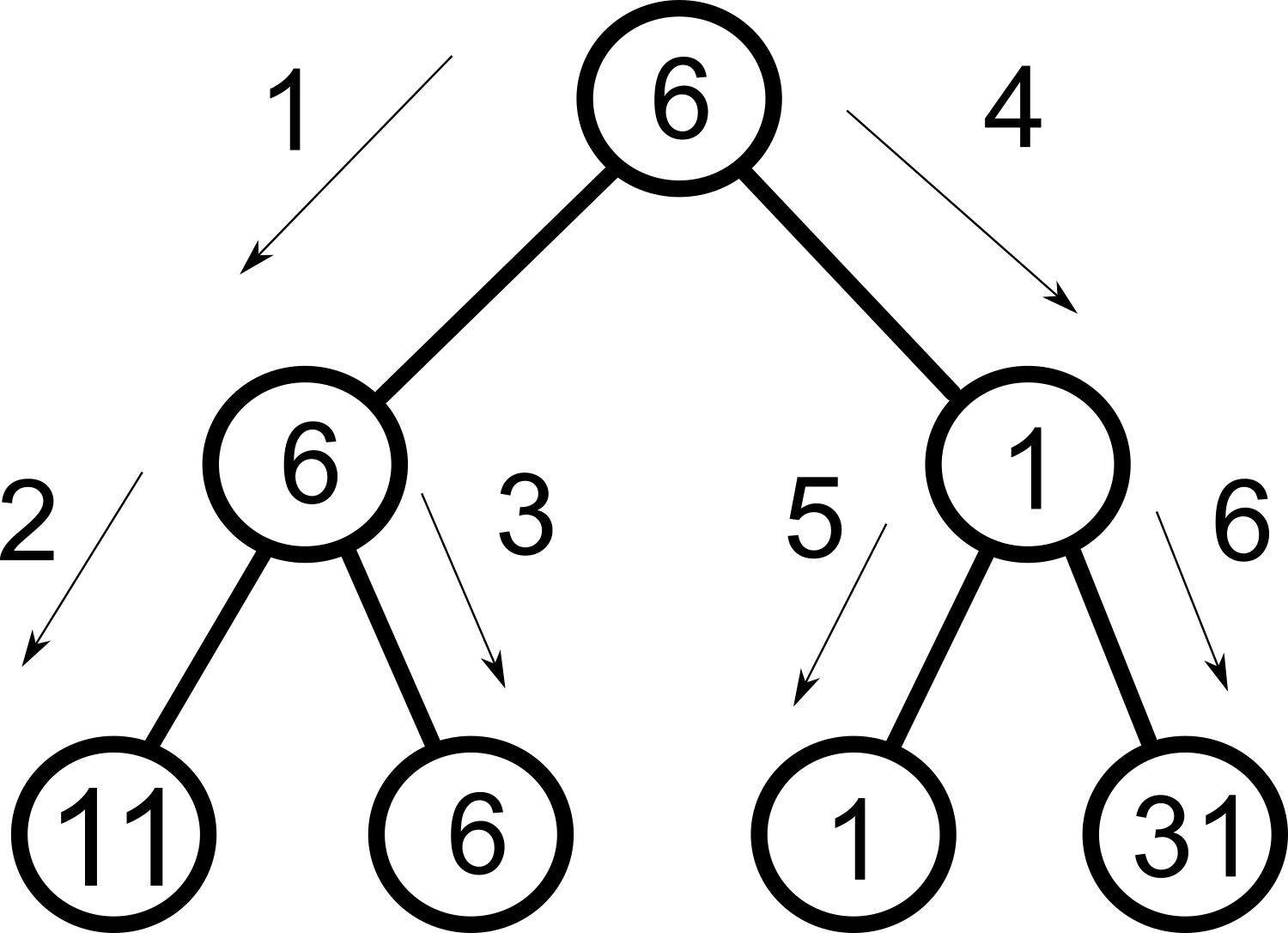
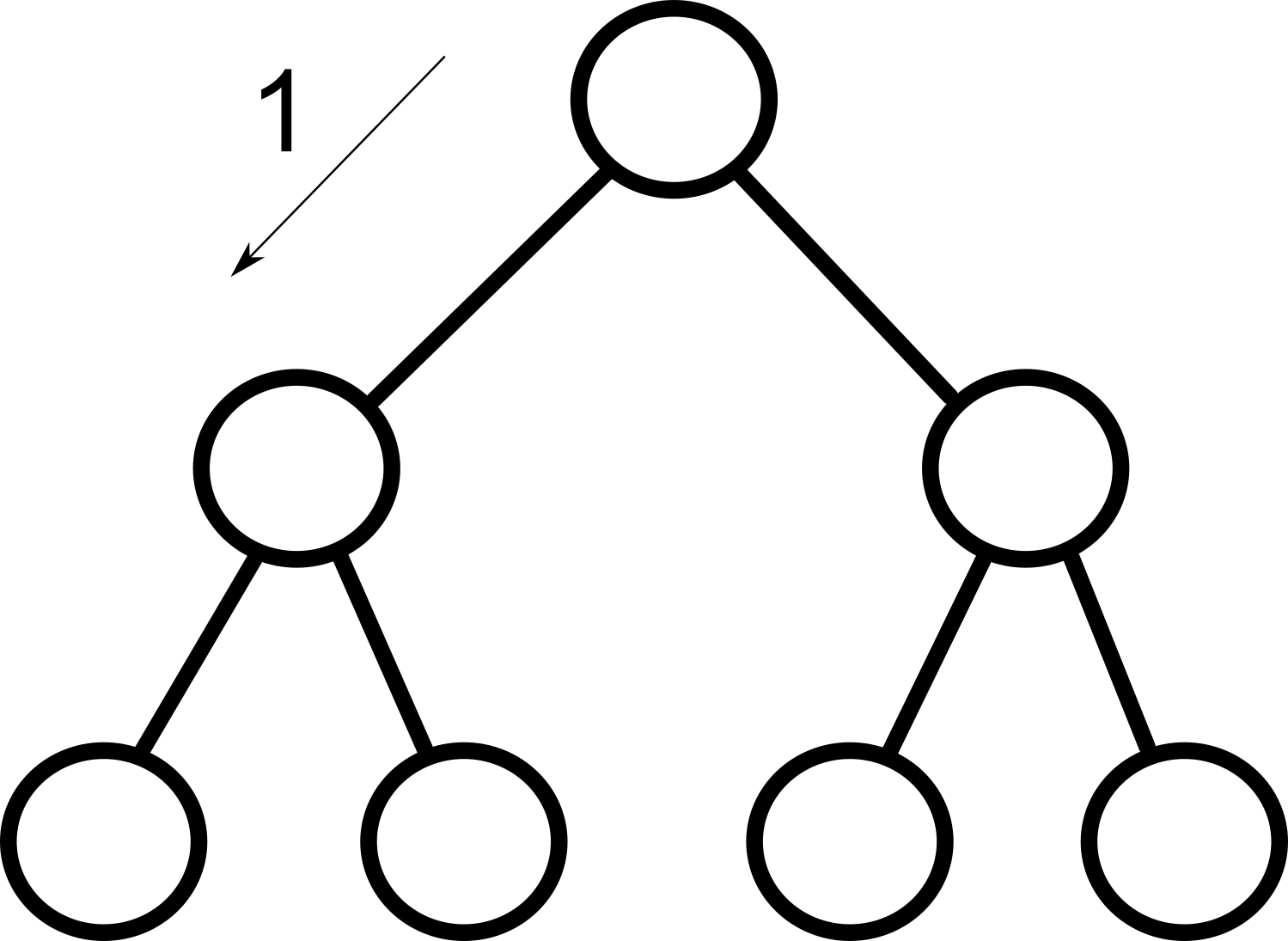

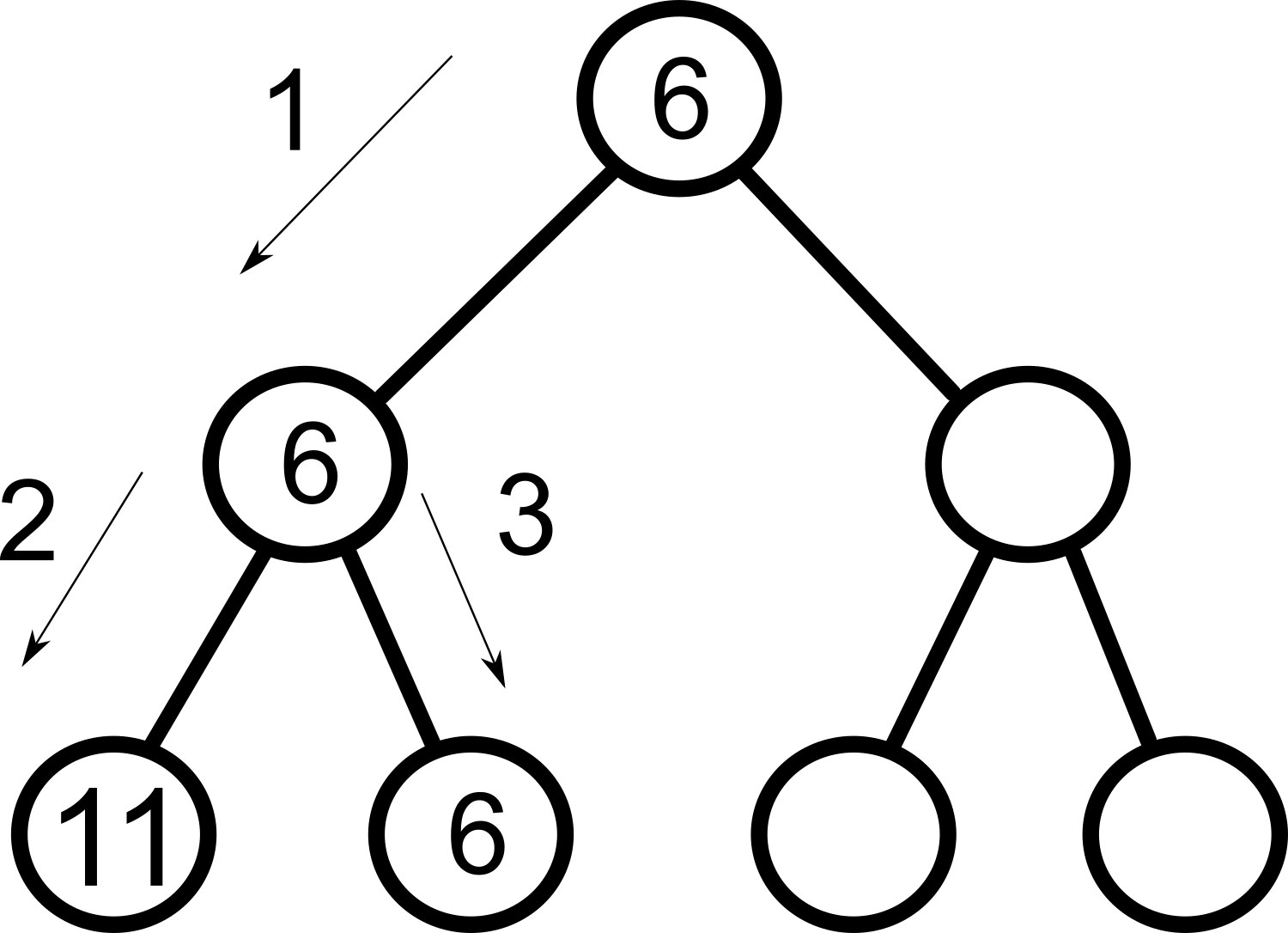
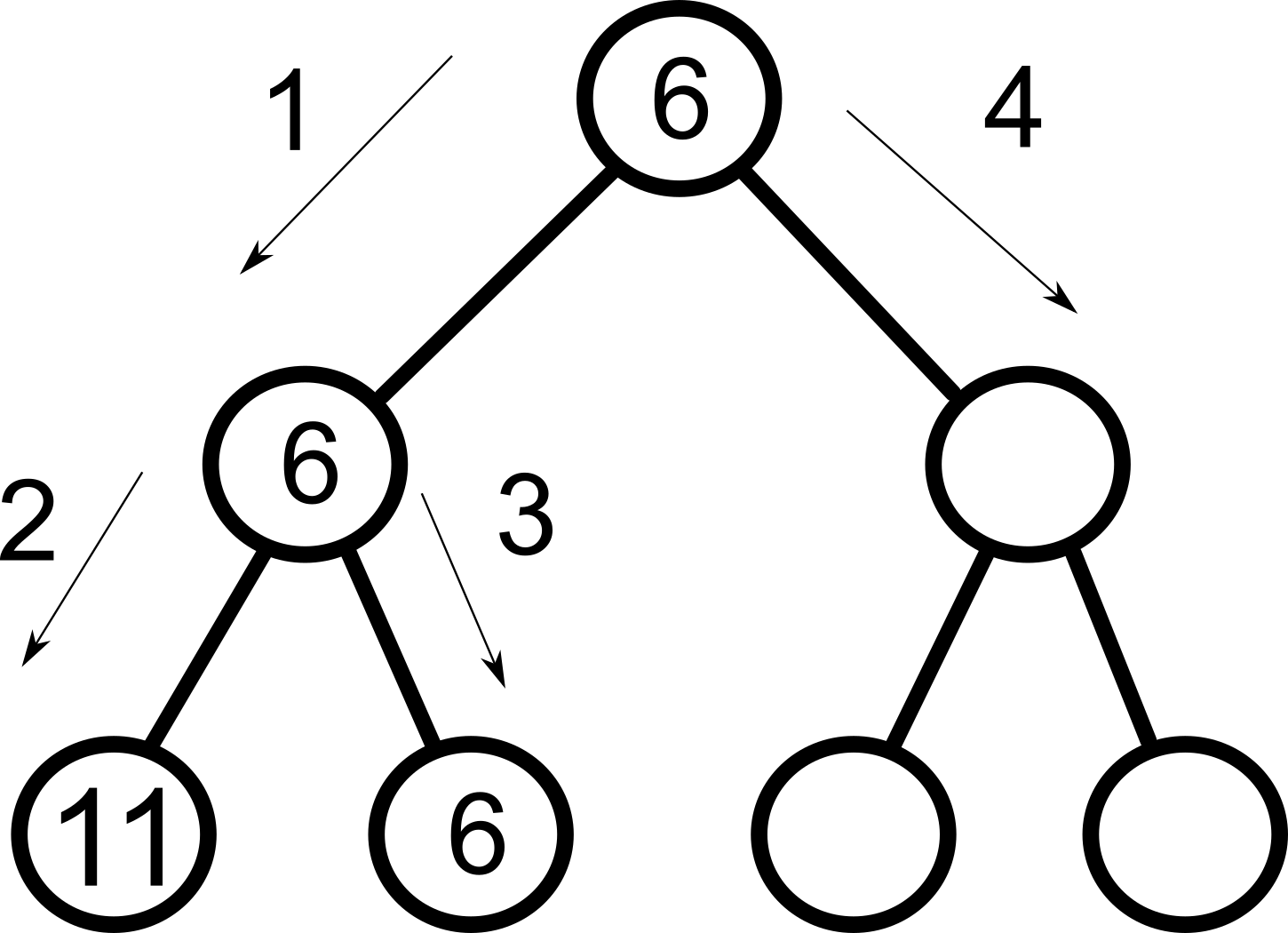
Vi kan alltså avbryta sökningen i detta delträd och spara en massa tid.
Vi kör ett exempel till. Vi dyker ner i vårt träd och finner 1 poäng.
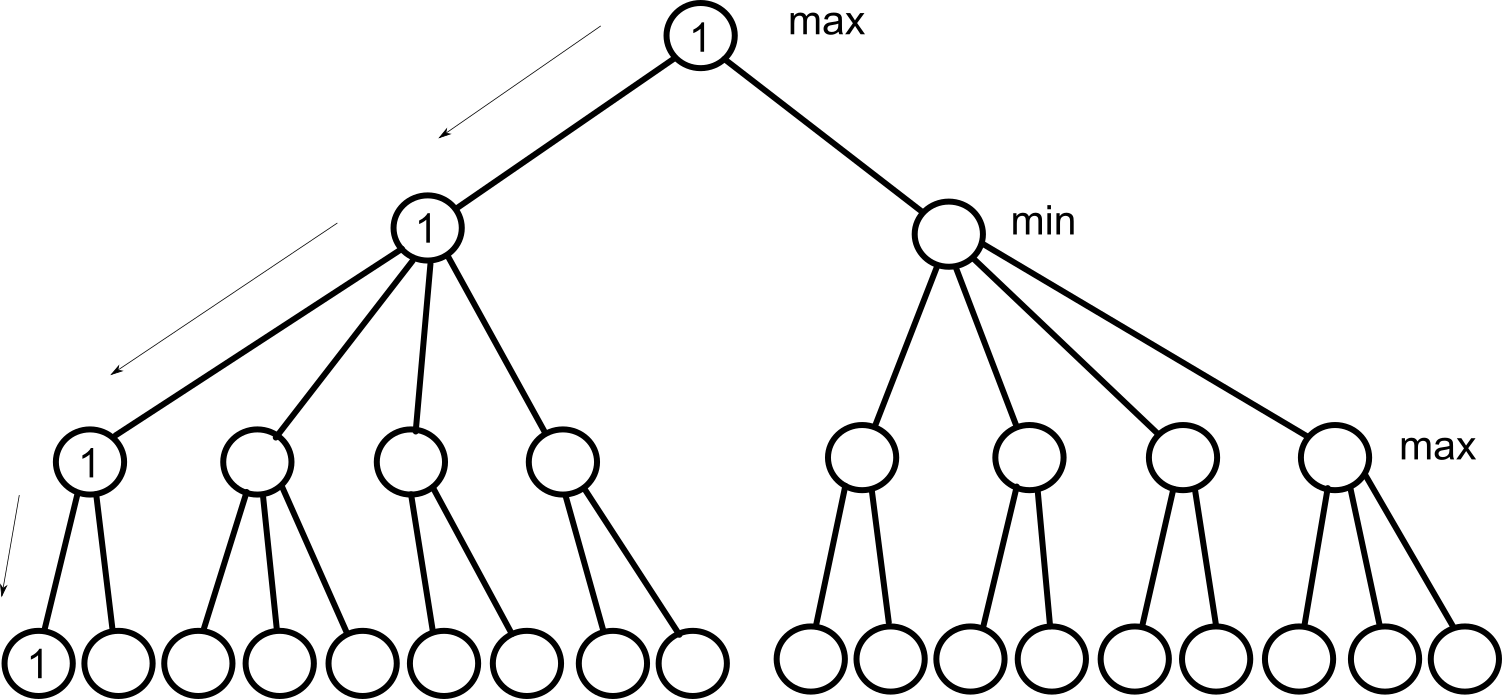


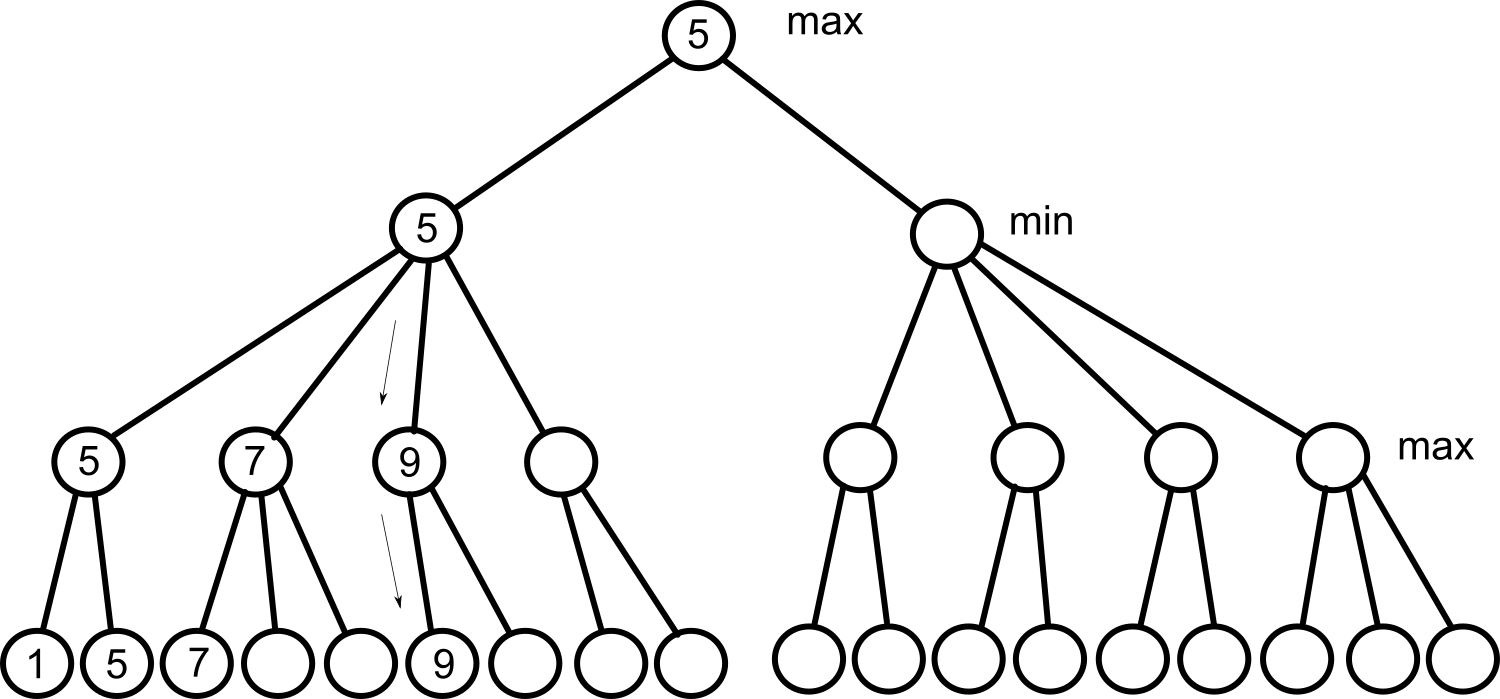
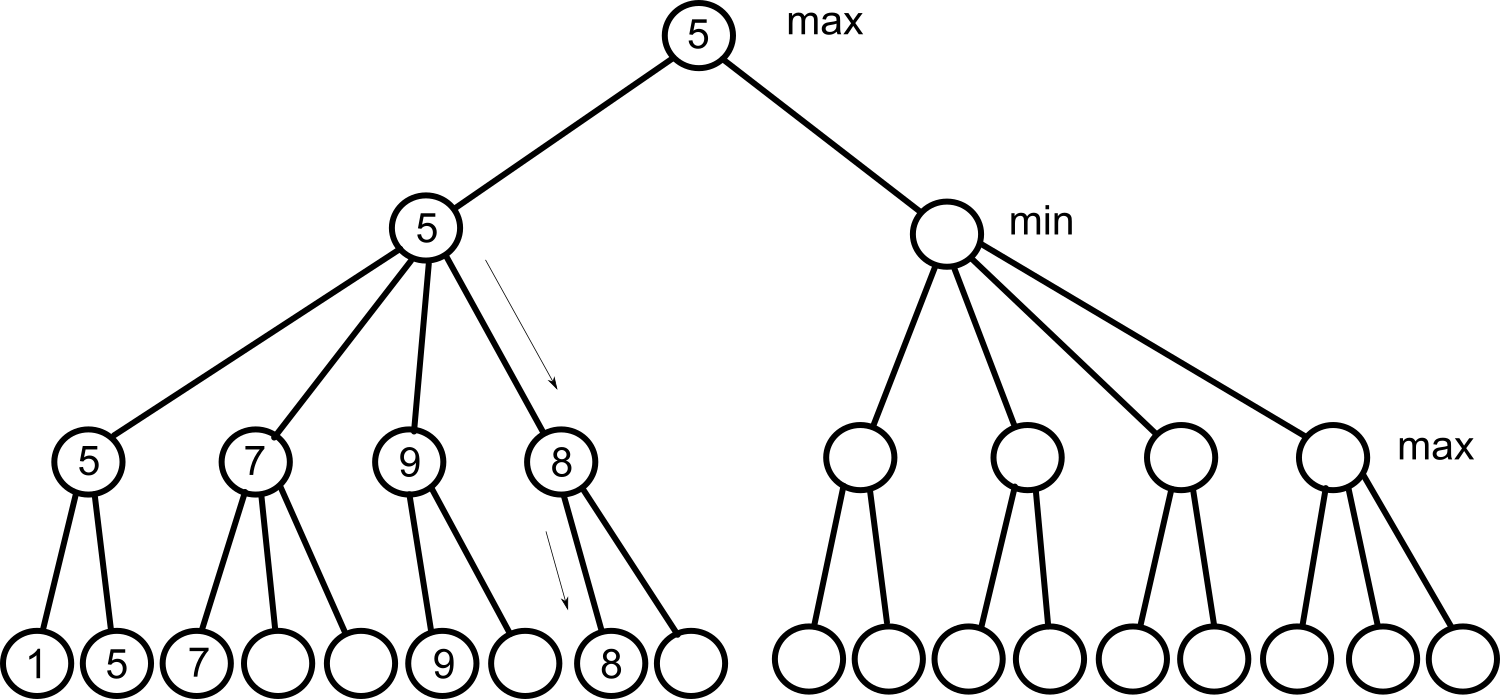

alfa och beta
alfa
Alfa är det minsta värde som vi efter en sökning är garanterade. Det kan bli högre om motspelaren gör dåligt ifrån sig. Men det kommer minst bli detta alfa-värde. Alfa representerar den minsta poäng som den maximerande ("vi") spelaren är garanterad.
beta
Beta är det högsta värde som vi efter en sökning kan uppnå. Beta är den högsta poäng som den minimerade spelaren (motspelaren) är garanterad.
negamax med alfabeta -reducering
För att skriva om negamax så att den arbetar med alfabeta -reducering behöver vi dels skicka med alfa och beta som parametrar. Dessutom lägga till två if -statser, den ena gör ett beta -klipp, den andra lagrar undan alfa -värdet. Vi byter plats på, dvs vänder på, logiken varannan nivå i trädet.
def NegaMaxAlfaBeta(djup, alfa, beta): if (djup == 0): return Eval() drag = dragGenerator while (drag kvar): Gör ett drag i listan val = -NegaMaxAlfaBeta(djup-1, -beta, -alfa) Ta tillbaka draget if (val >= beta): return beta if (val > alfa): alfa = val return alfa
För att testa om ovan pseudokod verkligen fungerar, så kan vi åter ta fram vårt lilla träd och köra negamax -algoritmen på det. Ändra värden i trädet och studera resultatet!
Negamax alfabeta
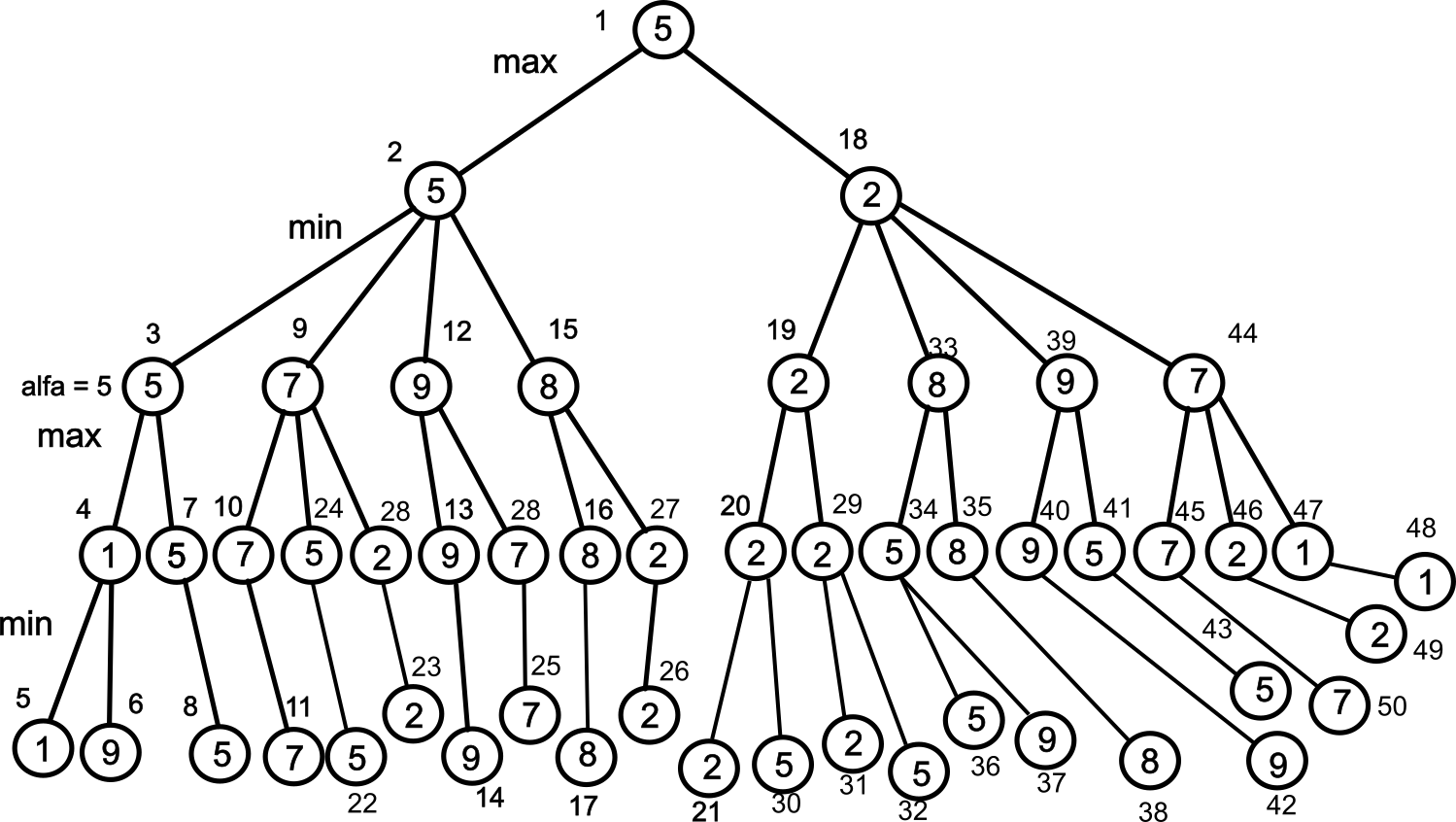
class Tree(object):
def __init__(self, name='r', data=None, children=None):
self.name = name
self.data = data
self.children = []
if children is not None:
for child in children:
self.add_child(child)
def add_child(self, node):
self.children.append(node)
def print_tree(tree, d=0):
for child in tree.children:
print("\n" + " "*d, end="")
print(child.name+'('+str(child.data)+')',end="->")
if(child.children):
print_tree(child,d+1)
#testa hur många noder som söks igenom
noder = 0
def negamax(tree, d):
global noder
noder=noder+1
if d > 3:
return(tree.data)
if tree.children is not None:
best = -999
for child in tree.children:
val = -negamax(child,d+1)
if(val > best):
best = val
child.data = val
return(best)
def negamax_alfabeta(tree, d, alfa, beta):
global noder
noder=noder+1
if d > 3:
return(tree.data)
if tree.children is not None:
for child in tree.children:
val = -negamax_alfabeta(child,d+1, -beta, -alfa)
child.data = val
if(val>=beta):
return(beta)
if(val>alfa):
alfa = val
return(alfa)
game = Tree('1', None,
[
Tree('2',None, [
Tree('3',None, [
Tree('4',None, [
Tree('5',1),
Tree('6',9)
]),
Tree('7',None, [
Tree('8',5)
])
]),
Tree('9',None, [
Tree('10',None, [
Tree('11',7)
]),
Tree('24',None,[
Tree('22',5)]),
Tree('51',None,[
Tree('23',2)])
]),
Tree('12',None, [
Tree('13',None, [
Tree('14',9)
]),
Tree('28',None,[
Tree('25',7)])
]),
Tree('15',None, [
Tree('16',None, [
Tree('17',8)
]),
Tree('27',None,[
Tree('26',2)])
])
]),
Tree('18',None, [
Tree('19',None, [
Tree('20',None, [
Tree('21',2),
Tree('30',5)
]),
Tree('29',None, [
Tree('31',2),
Tree('32',5)
])
]),
Tree('33',None,[
Tree('34',None, [
Tree('36',5),
Tree('37',9)
]),
Tree('35',None,[
Tree('38',8)])
]),
Tree('39',None,[
Tree('40',None, [
Tree('42',9)
]),
Tree('41',None,[
Tree('43',5)])
]),
Tree('44',None,[
Tree('45',None, [
Tree('50',7)
]),
Tree('46',None,[
Tree('49',2)]),
Tree('47',None,[
Tree('48',1)])
])
])
])
x = negamax_alfabeta(game,0, -99999999, 99999999)
#x = negamax(game,0)
print("Bästa värde:", x)
print_tree(game)
print("\nnoder",noder)
Som du ser ovan när du kör koden, så skippar den ganska många delträd men kommer fram till samma resultat. Prova köra med och utan alfabeta. Det står None på värdet, där negamax skippat delträd. Jämför utan alfabeta.
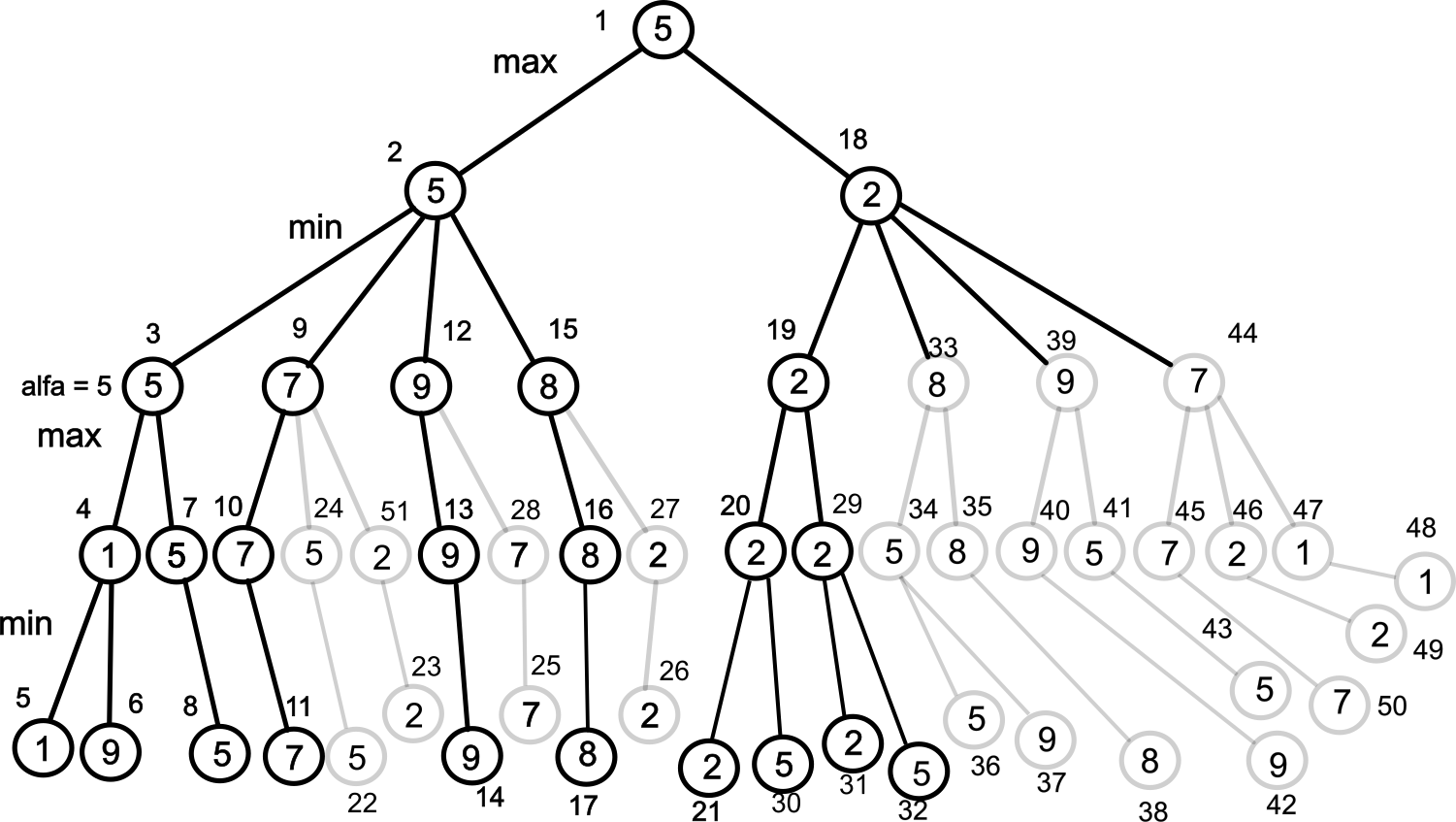
I ovan experiment -träd så klipps ungefär 50% bort när vi kör alfabeta -reducering jämfört med vanilla negamax. Men i verkligen, om förgreningsfaktorn är stor, så blir besparingen typiskt mycket större. Optimalt reduceras trädet med alfabeta till BD/2 + BD/2 - 1 (Knuth & Moore, 1975), där D är djupet och B är förgreningsfaktorn. Om man söker 2 ply fram och förgreningsfaktorn är 30, så med minimax genomsöks då 30*30 noder = 900 noder. Med alfabeta -reducering så genomsöks under optimala omständigheter, dvs perfekt dragsortering, 301+301-1 = 59 noder. Det är stor skillnad mellan 59 noder och 900 noder. Då är detta ett litet exempel. Det sticker iväg mot 99% vid lite större exempel. Det är alltså dumt att inte använda alfabeta -reducering. Men det förutsätter att du använder dragsortering, vilket lyckligtvis är ganska okomplicerat.

egenskaper
Ju större sökträd desto mer kan sparas med alfabeta -reducering. Ju tidigare vi upptäcker att vi kan klippa i trädet, desto mer kan vi klippa bort. Pga detta spelar dragsortering en stor roll, dvs att vi sorterar dragen så att beta -klippet kommer så tidigt som möjligt. Vi kan göra detta genom att i schack som exempel lägga drag som slår ut andra pjäser först i draglistan. Det är en enkel sortering som ger väldigt stor effekt på hur mycket som kan klippas bort i sökträdet.I ovan experiment -träd så klipps ungefär 50% bort när vi kör alfabeta -reducering jämfört med vanilla negamax. Men i verkligen, om förgreningsfaktorn är stor, så blir besparingen typiskt mycket större. Optimalt reduceras trädet med alfabeta till BD/2 + BD/2 - 1 (Knuth & Moore, 1975), där D är djupet och B är förgreningsfaktorn. Om man söker 2 ply fram och förgreningsfaktorn är 30, så med minimax genomsöks då 30*30 noder = 900 noder. Med alfabeta -reducering så genomsöks under optimala omständigheter, dvs perfekt dragsortering, 301+301-1 = 59 noder. Det är stor skillnad mellan 59 noder och 900 noder. Då är detta ett litet exempel. Det sticker iväg mot 99% vid lite större exempel. Det är alltså dumt att inte använda alfabeta -reducering. Men det förutsätter att du använder dragsortering, vilket lyckligtvis är ganska okomplicerat.