Algoritm naturliga logaritmen
Algoritm för att räkna ut naturliga logaritmen, dvs log i python.
Taylorserie för log(x)
Hur fungerar det när en miniräknare eller dator plockar fram naturliga logaritmen? Det görs genom att använda en taylorserie (länk öppnas nytt fönster) som itererar sig fram till ett tillräckligt exakt värde. Ju mer exakt man önskar desto fler iterationer behövs och desto längre tid tar det förstås.För tal |x| < 1 fungerar ...
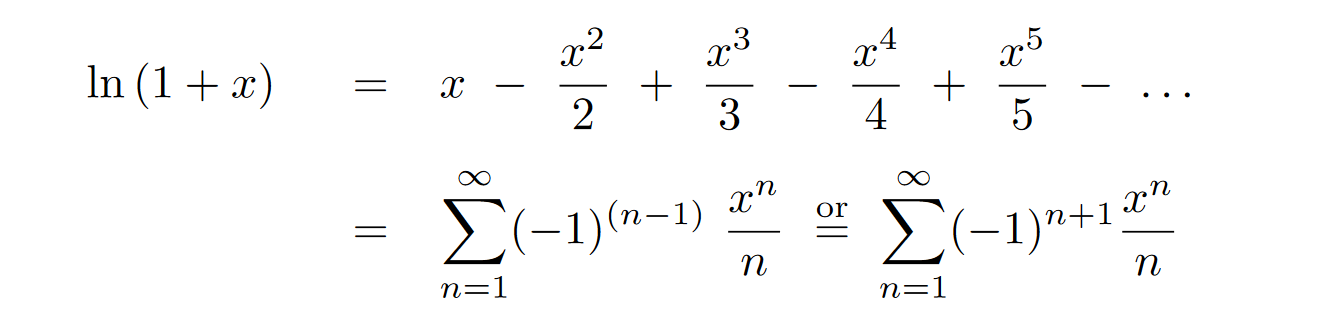
log, log10, ln och python
Ofta brukar det funka så på en minräknare att log motsvarar logaritm med 10 som bas och ln motsvarar e som bas.I python är log samma sak som ln, dvs e som bas. Sedan har man log10 för att funka som log med 10 som bas.
Titta på räknaren nedan, i övre högra hörnet av knapparna. På sätt och vis föredömligt och troligtvis också som det ser ut på din räknare också. Där hittar du funktionen ln på samma knapp som ex respektive log på samma knapp som 10x. Men i python är det alltså log (e som bas) respektive log10 (10 som bas) som gäller.

Algoritmen nedan fungerar för |x| < 1
OBS. I nedan kod är math inkluderat enbart för att kunna få ett jämförelsevärde. Observera att om du experimenterar för mycket med ett stort tal på iterationer, så kommer det kanske ta väldigt lång tid och din webbläsare kommer "hänga" sig.
import math
def log(x):
x = x - 1
it = 30
s = 0
t = -1
for i in range(1, it):
t = -t
s = s + t*x**i/i
return(s)
# denna kodrad borde python lagt in
ln = log
print(round(ln(0.5),5))
print(round(log(0.5),5))
print(round(math.log(0.5),5))