Pjäser & spelplan schack

binära egenskaper

Det är nödvändigt att du förstår vad som menas med bitvis logik för att begripa något här. Om du är lite ringrostig på detta, för det var ju ett tag sedan du kodade ditt egna operativsystem, gå tillbaka och kolla.

Man kan välja sättet att koda pjäserna, så att vi samtidigt ger dem binära egenskaper som är väldigt användbara bl.a. för att ta fram vilka legala drag som är möjliga.

♙	♘	♖	♗	♕	♔
Bonde	Häst	Torn	Löpare	Drottning	Kung
1	2	4	8	12	3
0001	0010	0100	1000	1100	0011
1	2	4	8	C	3

Vissa pjäser glider fram på schackbrädan (torn, löpare, drottning) och andra går bara ett steg (häst, kung samt bonde (bode är ett speciellt avsnitt)). Så vi kan namnge pjäserna så att bitarna berättar om pjäsens egenskaper. Så de 2 första bitarna avser pjäser som går 1 steg eller hoppar 1 steg. Medans bit 3 och 4 avser pjäser som glider fram.

Pjäser binära tal

Vidare vill vi förstås skilja på svart och vit. Det kan vi göra vi med bit 5 och 6.

	Vit	(binärt)	Svart	(binärt)
♙Bonde	0x11	0001 0001	0x21	0010 0001
♘ Häst	0x12	0001 0010	0x22	0010 0010
♗ Löpare	0x18	0001 1000	0x28	0010 1000
♖ Torn	0x14	0001 0100	0x24	0010 0100
♕ Drottning	0x1C	0001 1100	0x2C	0010 1100
♔ Kung	0x13	0001 0011	0x23	0010 0011

Ytterligare en viktig detalj, det är ju att i schack (och andra spel) så gäller vissa regler för en pjäs enbart om den tidigare inte har flyttat. T.ex. får en kung inte göra rokad om den flyttat på sig. En bonde får flytta 2 steg första gången, därefter enbart 1 steg. Så vi måste ge varje pjäs en minnesbit som är 0 från början, men blir 1 efter första gången pjäsen rört på sig. Då kan vi senare lätt skilja på regler som gäller före och efter den rört på sig. Bit 7 får vara denna bit, dvs sättas 1 om pjäsen rört på sig.

koda spelplan

Ett uppenbart sätt koda en spelplan är förstås att tänka sig en matris 8x8 rutor (array, 2d -lista). Schack spelas ju på 8x8 rutor, så uppenbart kodar vi det som 8x8 rutor. En logisk fortsättning på det uppenbara är att snickra på en drag-generator. Vi tänker oss då att om man numrerar alla positioner, så kan genom att lägga till och dra bort, hitta dragen för alla pjäser. Fint!

Dvs, fint, till vi upptäcker att det är ett skitsvårt problem veta om vi hamnar utanför spelplanen när vi drar bort och lägger till värden. Denna "lilla" detalj förstör tyvär allting.

Det visar sig, om man klurar en lång stund, att det finns en lösning på detta. Eller snarare; det finns flera. En av de bättre går under namnet 0x88. Poängen med 0x88 begrips om vi tänker oss en spelplan som är 16 rutor x 8 rutor. Vi struntar förstås i den ena halvan när vi spelar.



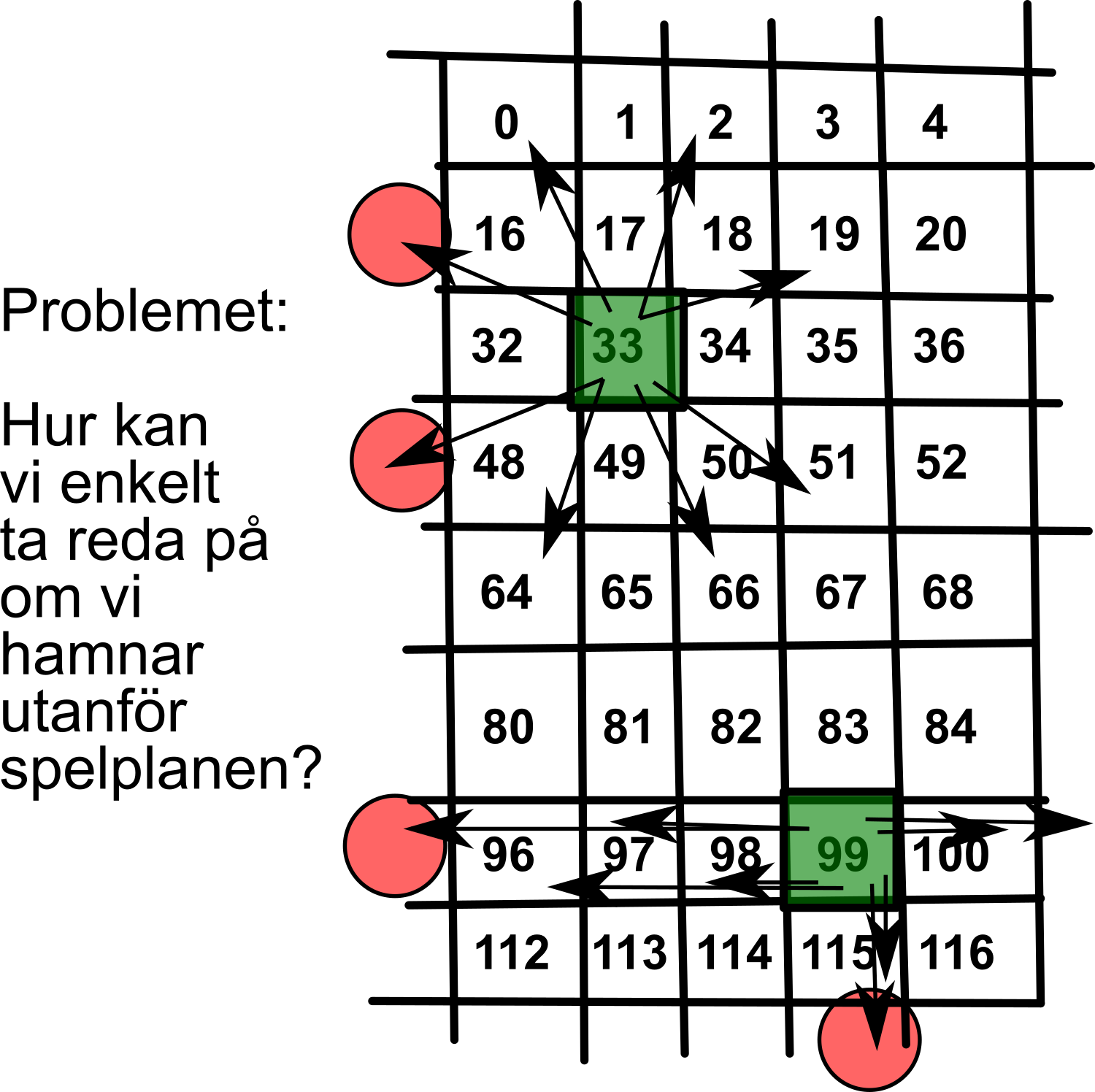
Tanken är inte att hitta på en ny typ av schack. Men internt i programmet representerar vi spelplanen 16x8 rutor och syftet med detta blir klart om vi tittar på de binära talen för siffrorna 0-128 arrangerade så att det blir 16x8 rutor.



Om vi printar ut talen 0-127 på binärt format och för utskriftens skull skippar de 4 mest signifikatna bitarna, så ser det ut såhär.



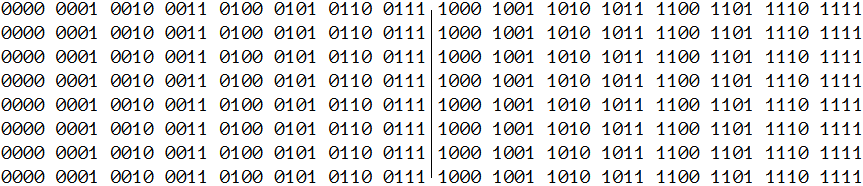
Det går också köra denna kod och titta. Klicka på koden och maximera fönstret.

Vad ser vi? Vi ser att om vi tänker oss att vi gör våra plus och minus för att räkna ut vart en spelpjäs kan hamna, så betyder "utanför spelplanen" att bit 4 blir 1. Bit 4:a om man ser det hela hexadecimalt 0x08. I själva verket finns en situation när man subtraherar för mycket och hamnar utanför spelplanen och talet blir negativt. Då blir MSB biten 1 (utanför vad som syns här). Därför är denna teknik döpt till 0x88. Dvs, vi kan plussa och subtrahera för att leta positioner för pjäserna. Vi kan sedan testa siffran med bitvis logik mot 0x88, för att blixtsnabbt se om vi hamnar utanför spelplanen. Isåfall struntar vi bara i det värdet.



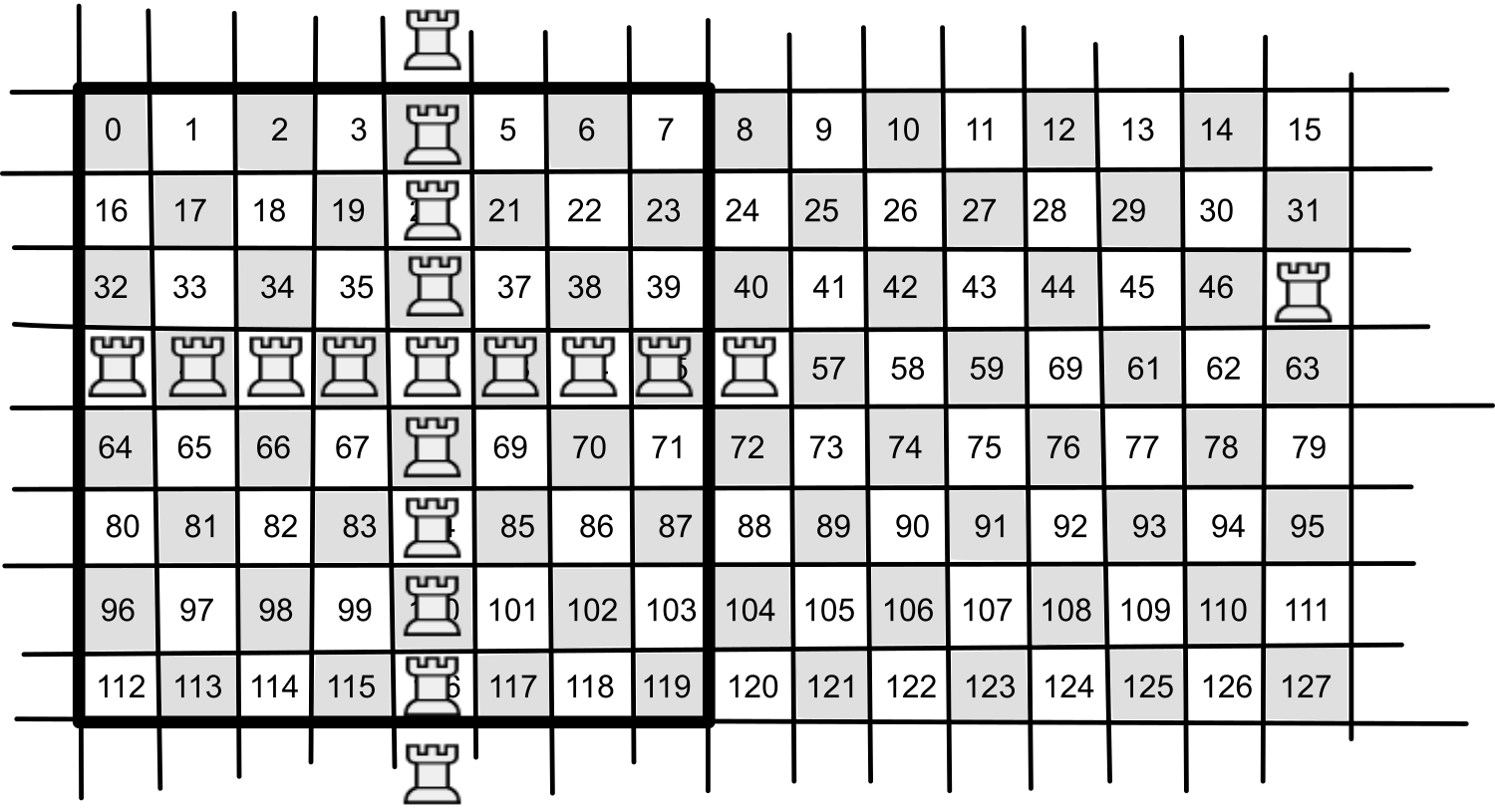
Vi kodar lite för att ge ett exempel. Ta hästen som exempel. Vi ställer en ensam häst 0x22 på position 51 nedan. Sen vill vi räkna ut vilka positioner denna kan flytta till. Vi kan enkelt räkna ut att alla offset blir [-33,-31,-14,-18,14,31,33,18] relativt den position vi står på.

I ovan exempel så står hästen stabilt mitt inne i spelplanen. Så ingenting behöver filtreras bort med 0x88.

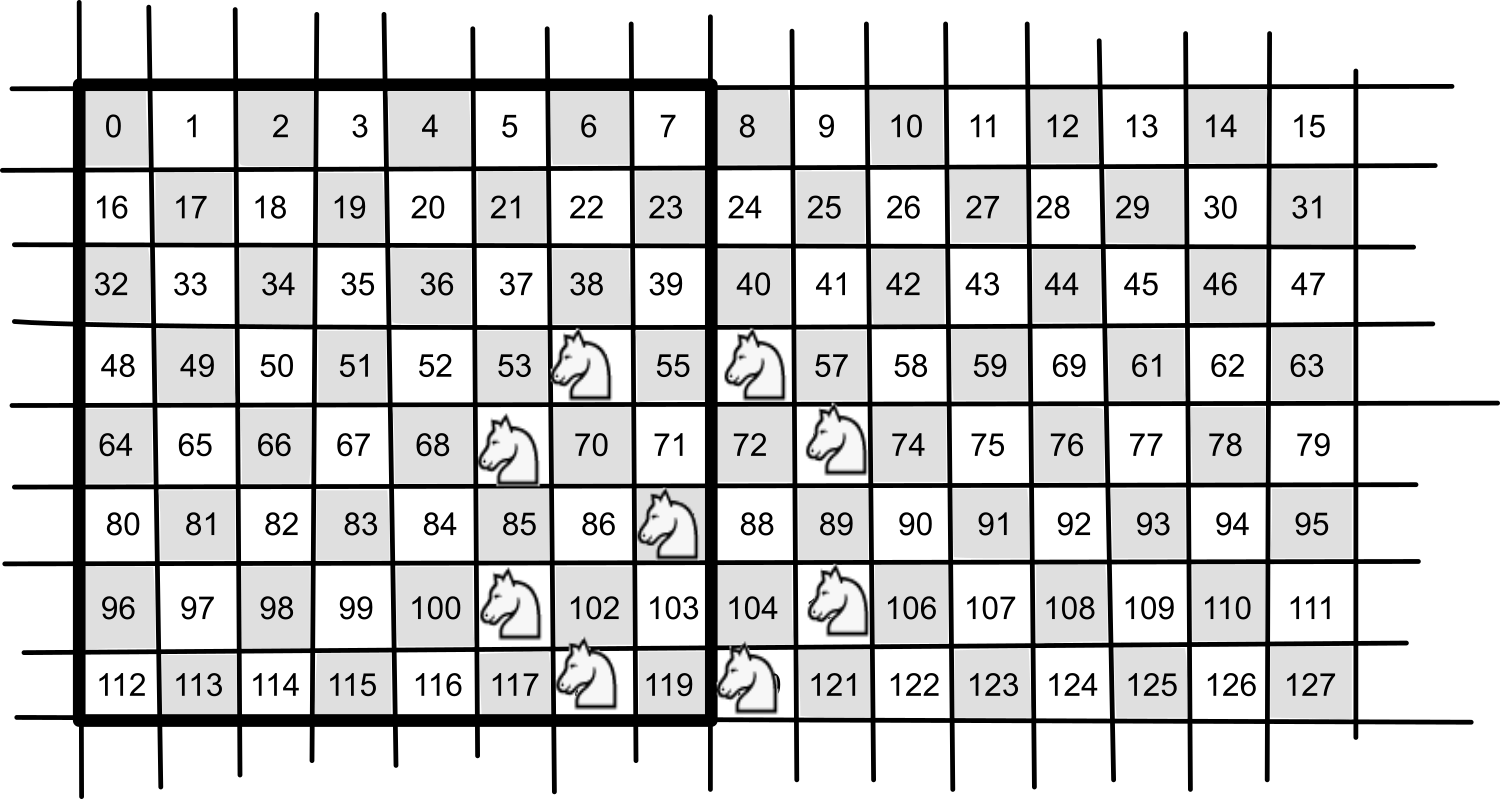
Vi kan ta ett exempel till. Vi ställer hästen till höger på spelplanen.

Om du räknar på positionerna vi får efter rensning med 0x88, så är det klockrent. Alla knas-positioner försvinner och kvar är de som ligger på spelplanen. Mycket effektivt!



Sensmoralen är följande: Vi behöver en spelplan som är 16x8 rutor, för att kunna använda 0x88 -metoden.

Så, det är vad vi gör.