Egna operatorer i postfix
Det går förstås att enkelt skapa egna operatorer i postfix-algoritmen. Förutom de 4 räknesätten kan man tänka sig de logiska operatorerna, mängdoperatorer, eller t.ex. operatorer för seriell och parallell -koppling av elektroniska komponenter !
Operatorer för att beskriva kretsar
Så, nedan har jag dels skapat 2 operatorer s och p. Det står för s=seriekopplat och p=parallellkopplat. Utöver det har jag gjort så att operander kan ges enheter. På så vis kan man samtidigt avgöra om det är resistanser, kondensatorer eller spolar.Det är önskvärt kunna skriva "matematiska" uttryck av typen nedan, vilka beskriver en elektrisk krets med seriekopplade och/eller parallellkopplade resistanser, kondensatorer och spolar.
(955mH s (10uF p (636uF s 1kohm))) p 636uF s 6ohm
Så, om vi t.ex. kör 12 volt med 50Hz AC genom ovanstående härva av motstånd, kondingar och spolar, vad blir strömmen I= ?
import re
import math
freq = 50
stack = []
def is_number(n):
try:
float(n)
except:
return False
return True
def prec(c):
if(c=='R' or c=='C' or c=='L'):
return(4)
if(c=='*'):
return(3)
if(c =='p'):
return(2)
if(c =='s'):
return(1)
return(0)
def infix2postfix(uttryck):
postfix = []
uttryck = uttryck.lower()
uttryck = uttryck.replace("kohm", "*1000R")
uttryck = uttryck.replace("mohm", "*1000000R")
uttryck = uttryck.replace("ohm", "*1R")
uttryck = uttryck.replace("mh", "*0.001L")
uttryck = uttryck.replace("mf", "*0.001C")
uttryck = uttryck.replace("uf", "*0.000001C")
uttryck = uttryck.replace("nf", "*0.000000001C")
uttryck = uttryck.replace(" ", "")
infix = re.findall(r'(R|L|C|s|p| |[0-9\.]+|\*|\+|\-|\/|\(|\))', uttryck)
infix_fixed=[]
for x in range(0,len(infix)):
if(infix[x]=='s' or infix[x]=='p' or infix[x]=='(' or infix[x]==')'):
infix_fixed.append(infix[x])
if(infix[x]=='R' or infix[x]=='C' or infix[x]=='L'):
infix_fixed.append(infix[x])
infix_fixed.append('(')
infix_fixed.append(infix[x-3])
infix_fixed.append(infix[x-2])
infix_fixed.append(infix[x-1])
infix_fixed.append(')')
for c in infix_fixed:
if(is_number(c)):
postfix.append(c)
elif(c=='('):
stack.append('(')
elif(c==')'):
while(stack[-1]!='('):
postfix.append(stack[-1])
stack.pop()
stack.pop()
else:
while(len(stack) > 0 and prec(c) <= prec(stack[-1])):
postfix.append(stack[-1])
stack.pop()
stack.append(c)
while(len(stack) != 0):
postfix.append(stack[-1])
stack.pop()
return(postfix)
def operator(n):
if(len(n)==1):
return(prec(n))
else:
return(0)
def evalPostfix(postfix):
for e in postfix:
if(operator(e)):
b = complex(stack[-1])
stack.pop()
if(len(stack)>0):
a = complex(stack[-1])
stack.pop()
else:
a=complex(0,0)
if(e=='R'):
if(a!=complex(0,0)):
stack.append(str(a))
stack.append(str(b))
if(e=='C'):
if(a!=complex(0,0)):
stack.append(str(a))
Xc = 1/(2*math.pi*freq*b)
stack.append(str(complex(0,-Xc)))
if(e=='L'):
if(a!=complex(0,0)):
stack.append(str(a))
Xl = 2*math.pi*freq*b
stack.append(str(complex(0,Xl)))
if(e=='s'):
stack.append(str(a+b))
if(e=='p'):
stack.append(str(1/(1/a+1/b)))
if(e=='*'):
stack.append(str(a*b))
else:
stack.append(e)
return(complex(stack[0]))
def arg(C):
alfa = math.atan(C.imag/C.real)
return(math.degrees(alfa))
uttryck = " (955 mH s (10 uF p (636 uF s 1 kohm))) p 636uF s 6 ohm "
postfix = infix2postfix(uttryck)
z = evalPostfix(postfix)
u = 12
i = u/z
print("I=",abs(i))
print("arg=",arg(i))
Det här var alltså kretsen. 1.49 A samt ca 39 graders fasskillnad mellan ström och spänning.
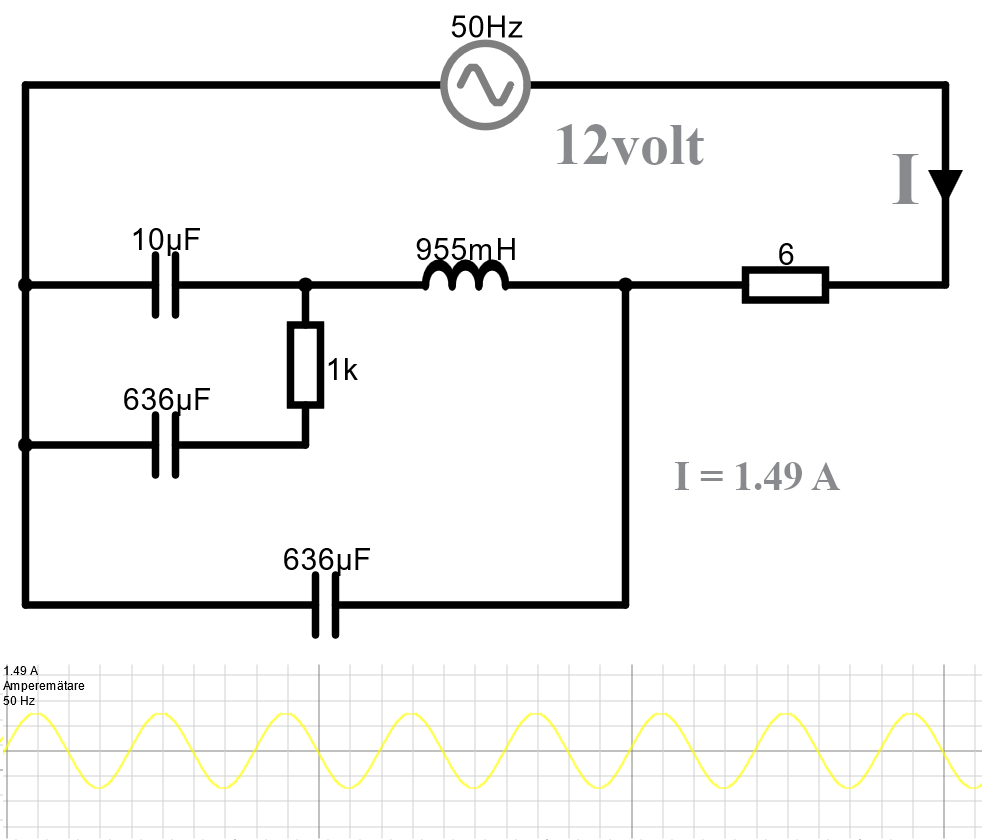
Dubbelkolla i krets simulator. På sätt och vis en smula magiskt att det faktiskt stämmer. Science!

Dubbelkolla i krets simulator. På sätt och vis en smula magiskt att det faktiskt stämmer. Science!