complex(x,y)
Skapar ett komplext tal givet realdelen i samt imaginärdelen j.
komplext tal
c= complex(5,4)
print(c)
För att omvänt komma åt realdelen och imaginärdelen i det komplexa talet ...
realdel och imaginärdel
c= complex(5,4)
print("real del=",c.real)
print("imaginär del=",c.imag)
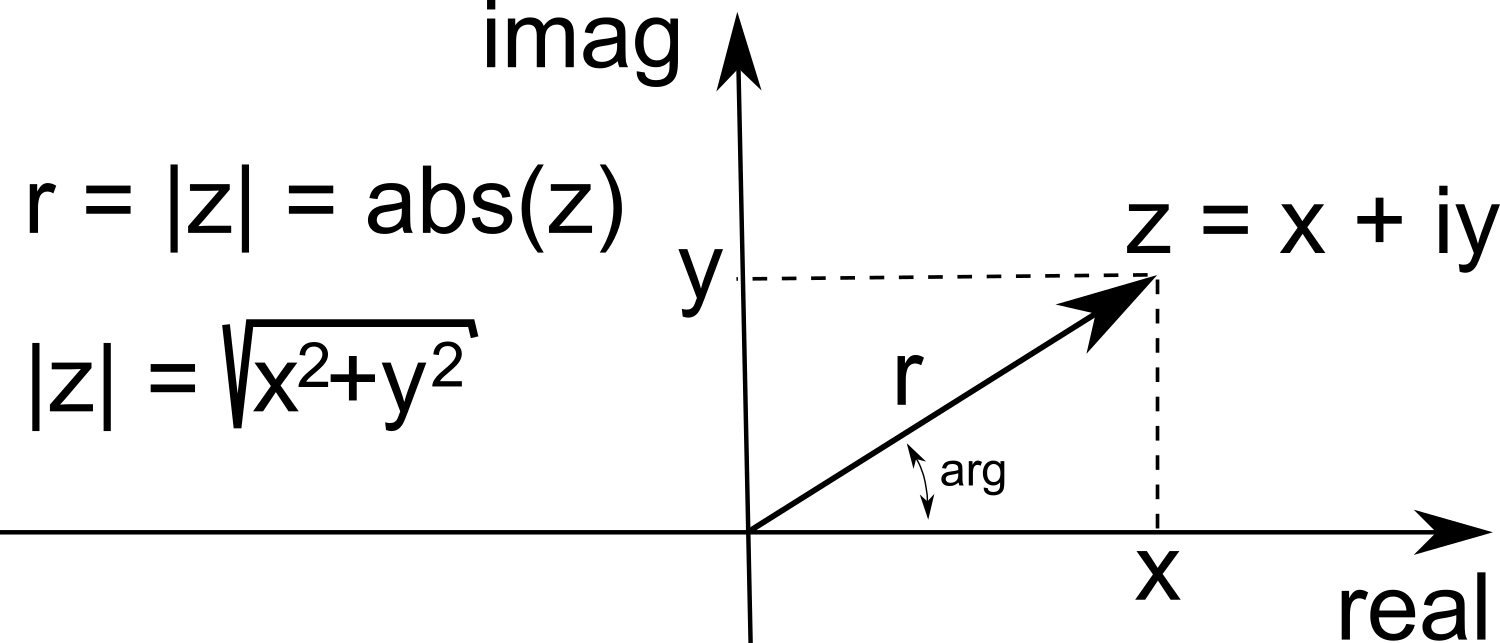
aritmetik med komplexa tal
Räknesätten fungerar som vanligt, fast med skillnaden att du använder komplexa tal. Summa av 2 komplexa tal.c1 = complex(3,0)
c2 = complex(0,4)
summa = c1 + c2
print("c1+c2=",summa)
print("real del=",summa.real)
print("imaginär del=",summa.imag)
print("absolutbeloppet=",abs(summa))
växelströmskretsar
För att räkna på växelströmskretsar med kondensatorer och spolar (induktorer) så kan vi representera komponenterna med komplexa tal (observera att du kan räkna om till/från reaktans med formlerna för reaktans XL=2πwL och XC=1/(2πwC).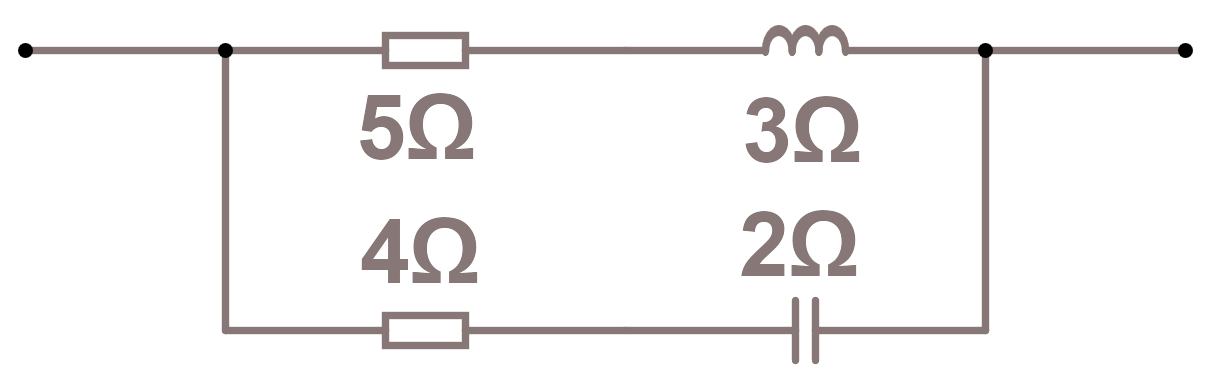
Seriekoppling, vi summerar alla R.


import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
def R(r):
return complex(r,0)
def I(z):
return complex(0,z)
def C(z):
return complex(0,-z)
def arg(C):
alfa = math.atan(C.imag/C.real)
return(math.degrees(alfa))
def iround(C,d):
return(complex(round(C.real,d),round(C.imag,d)))
z = parallell(serie(R(5),I(3)),serie(R(4),C(2)))
print("z=",iround(z,2))
print("|z|=",str(round(abs(z),2)),
" arg=",str(round(arg(z),2)),"grader")
Vi kan lägga till formlerna för reaktans direkt i koden, dvs XL=2πwL och XC=1/(2πwC), för respektive spole och kondensator och kan då ge dessa komponenters värden direkt i koden. Så i nedan schema är kondensatorn 636 µF och spolen är 9.6 mH. Uppgiften är då att beräkna strömmen (vars facit redan står i kretsschemat, då bilden kommer från krets-simulatorn)
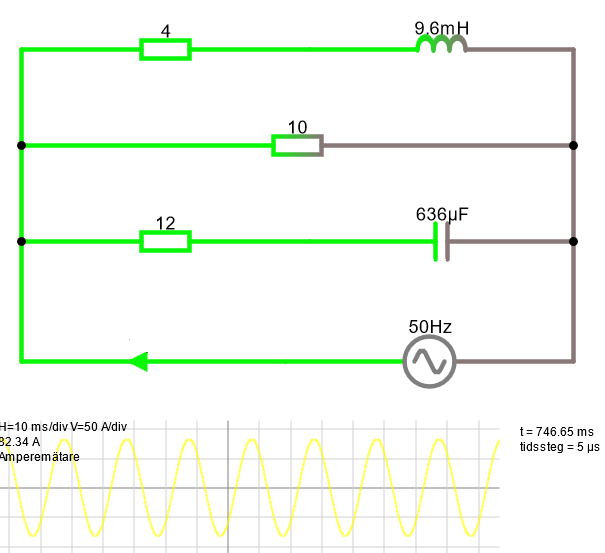

import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
def R(r):
return complex(r,0)
def I(z):
return complex(0,z)
def XI(L,f):
return (I(2*math.pi*f*L))
def C(z):
return complex(0,-z)
def XC(F,f):
return (C(1/(2*math.pi*f*F)))
def arg(C):
alfa = math.atan(C.imag/C.real)
return(math.degrees(alfa))
def iround(C,d):
return(complex(round(C.real,d),round(C.imag,d)))
z1 = serie(R(4), XI(0.00955,50))
z2 = R(10)
z3 = serie(R(12),XC(0.000636,50))
zres = parallell(z1,z2,z3)
i = 240/zres
print("i=",iround(i,2))
print("|i|=",str(round(abs(i),2)),
" arg=",str(round(arg(i),2)),"grader")