Bitvis logik
Bitvis logik syftar på operatorer som jobbar på talens bitmönster. Bitvis logik är regel snarare än undantag om vi pratar lågnivåprogrammering, t.ex. maskinkod. Men det kan också göra nytta i andra sammanhang.
bitvisa operatorer
| Operator | Tecken | Exempel |
| not | ~ | ~x |
| and | & | x&y |
| or | | | x|y |
| xor | ^ | x^y |
| skifta höger | >> | x>> |
| skifta vänster | << | x<< |
Låt oss arbeta med ett 8-bitars tal i några exempel. Positionerna värde nedan för respektive plats i siffran. Nedan tal är 70 = 64 + 4 + 2
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| MSB | LSB |
Låt oss samtidigt introducera begreppen MSB (Most Signifiant Bit, mest värdefulla) och LSB (Least Significant Bit, minst värdefulla). Det är vanligt att man pratar om MSB och LSB i olika sammanhang.
Bitvis & (and)
Bitvis and tar alltså och gör and bit för bit och bygger upp resultatet.
x = 64
y = 96
z = x&y
print(z)
print("{:0>8b}".format(z))
Det krävs alltså att samma bit är 1 i båda talen för att det skall bli 1 i resultatet.
Så svaret borde bli 64.
Vi gör samma grej med or.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| x=64 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| y=96 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| x&y | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Så svaret borde bli 64.
Om du glömt bort hur
print("{:0>8b}".format(z)) fungerar, kolla här.
Bitvis | (or)
Vi gör samma grej med or.
x = 66
y = 97
z = x|y
print(z)
print("{:0>8b}".format(z))
Vad händer här? Vi tar bitarna bitvis or. Dvs det räcker att vi har en bit 1 i något av talen för att få 1 i resultatet.
Svaret borde bli 64 + 32 + 2 + 1 = 99
XOR är lite klurigare förstå. Det xor gör, det är att på den position där y är 1, där inverteras x.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| x=66 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| y=97 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| x|y | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
Svaret borde bli 64 + 32 + 2 + 1 = 99
Bitvis ^ (xor)
XOR är lite klurigare förstå. Det xor gör, det är att på den position där y är 1, där inverteras x.
x = 73
y = 127
z = x^y
print(z)
print("{:0>8b}".format(z))
I fallet nedan när y = 127, vilket är ju är 0111 1111, så inverteras samtliga positioner i x.
Svaret borde bli 32 + 16 + 4 + 2 = 54
I ovan enkla fall så inverterade xor samtliga positioner (motsvarande 127 = 0111 1111). Men vi hade kunnat låta xor invertera varannan eller vilka godtyckliga bitar som helst. Xor är hörstenen i all modern kryptering. Exempel på kryptering.
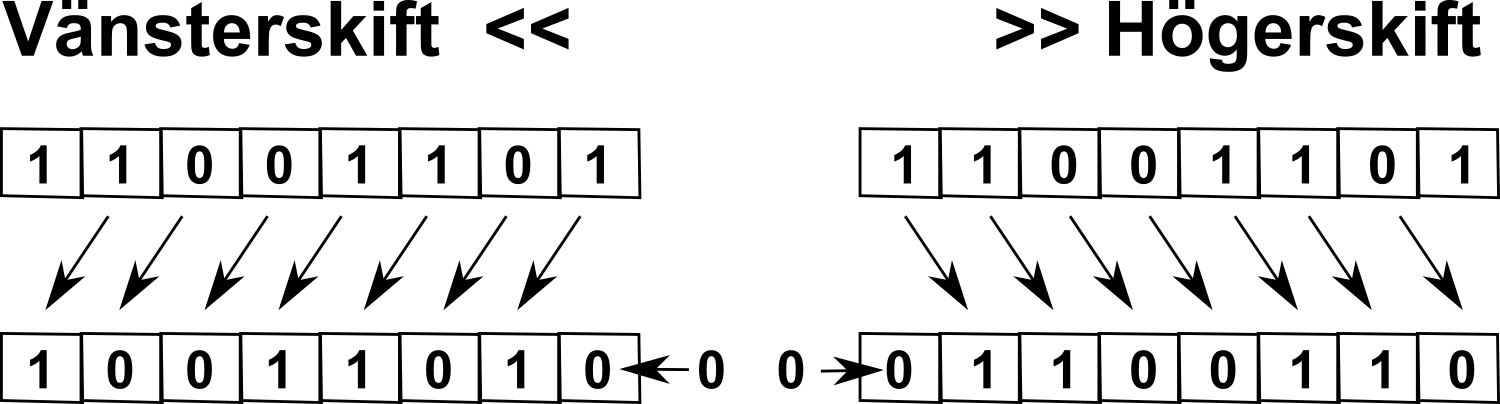
Högerskift flyttar alla bitar ett steg åt höger, det är vad 1an i koden nedan betyder. Man kan minnas högerskift genom att >> pekar åt höger. En av bitarna, den längst till höger, trillar över kanten och försvinner. En nolla knuffas in på vänster sida.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| x=73 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| y=127 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x^y | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
Svaret borde bli 32 + 16 + 4 + 2 = 54
I ovan enkla fall så inverterade xor samtliga positioner (motsvarande 127 = 0111 1111). Men vi hade kunnat låta xor invertera varannan eller vilka godtyckliga bitar som helst. Xor är hörstenen i all modern kryptering. Exempel på kryptering.
Högerskift x>>
Högerskift flyttar alla bitar ett steg åt höger, det är vad 1an i koden nedan betyder. Man kan minnas högerskift genom att >> pekar åt höger. En av bitarna, den längst till höger, trillar över kanten och försvinner. En nolla knuffas in på vänster sida.
x = 96
z = x>>1
print(z)
print("{:0>8b}".format(z))
Detta är samma sak som att dividera med 2.
Svaret borde bli 32 + 16 = 48
Vänsterskift flyttar alla bitar åt vänster. I nedan fall flyttar vi 1 steg, det är 1an i koden. Man kan minnas vänsterskift genom att << pekar åt vänster. En av bitarna, den längst till vänster, trillar över kanten och försvinner. En nolla knuffas in på höger sida.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| x=96 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| x>>1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Svaret borde bli 32 + 16 = 48
Vänsterskift x<<
Vänsterskift flyttar alla bitar åt vänster. I nedan fall flyttar vi 1 steg, det är 1an i koden. Man kan minnas vänsterskift genom att << pekar åt vänster. En av bitarna, den längst till vänster, trillar över kanten och försvinner. En nolla knuffas in på höger sida.
x = 96
z = x<<1
print(z)
print("{:0>8b}".format(z))
Flytta 1 steg åt vänster är samma sak som att multiplicera med 2.
Sammanfattningsvis ...
Bitvis not inverterar bitarna bitvis.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| x=96 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| x>>1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Sammanfattningsvis ...

Bitvis ~ (not)
Bitvis not inverterar bitarna bitvis.
x = 73
z = ~x
print(z)
print("{:0>8b}".format(z))
print()
print("{:0>8b}".format(73))
print("{:0>8b}".format(~73+256))
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| x=73 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| ~x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
Så vad är svaret här? Python säger -74. Vilket är helt riktigt. För att begripa bitvis not måste man känna till 2-komplement. För grejen är den att bitvis invertering kommer alltid invertera MSB till 1.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| ~x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
Den högsta biten här säger att talet är negativt. För att få återgå från 2-komplement och synliggöra siffran så inverterar vi alla bitar och lägger till 1, så ser vi det riktiga numret.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| ~x | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
Nu ser vi att det är 64 + 8 + 2 = 74 och ett minustecken på detta.